
函数依赖概念理解与判断
函数依赖:
符号表示:X→Y
定义:6.1设R(U)是属性集U.上的关系模式,X, Y是U的子集。若对于R(U)的任意
一个可能的关系r,r中不可能存在两个元组在X上的属性值相等,而在Y上的属性值不等,
则称X函数确定Y或Y函数依赖于X,记作X→Y。
理解定义:设X,Y为两个集合,对于集合X中的所有元素,在Y中都能得到对应。
①当X值不同时:X既可以对应Y的相同元素,也能对应不同元素。
②当X值相同时:X只能对应Y中的相同元素。
判断是否是函数依赖:
当然,偶认认真真读了几遍概念还是一脸懵逼QAQ但总不能不会,毕竟要还要应用,所以下面结合了比较容易理解的属性间的关系来使用它,也就是通过一对一、一对多、多对一、多对多的关系来判断两个集合是否存在依赖关系。
首先来死背下面3条关系:
1.X和Y是一对一的关系,则X→Y,Y→X
2.X和Y是多对一的关系,则X→Y
3.X和Y是多对多或是一对多的关系,则X与Y不存在依赖关系~
实例:对于表Student(sno,sname,ssex,cno,scourse,grade),先说明一个大前提,这里没有任何规定,因此默认姓名、课程名、分数和性别在表中允许存在相同的值,学号和课程号都不允许存在相同的值。
判断下列依赖关系是否正确:
①sno→sname ②sno→ssex ③(sno,sname)→scourse ④(sno,cno)→grade
①sno→sname:一个姓名可以决定多个学号,一个学号只能决定一个姓名,这里不要懵哇,想想,2个同名的人是不是有两个学号!!因此学号和姓名是多对一的关系,所以有sno→sname
②sno→ssex:一个性别可以决定多个学号,一个学号只能决定一个性别,所以有sno→ssex
③(sno,sname)→scourse:一个姓名和一个学号可以决定多门课程,一门课程决定多个学号和姓名选修,因为一个学生能够选修多门课程嘛,一门课程也能被多个学生选修,所以学号和姓名二者跟课程是多对多的关系,不存在函数依赖,不能得出(sno,sname)→scourse
④(sno,cno)→grade:一个姓名和一个课号可以决定一个分数,一个分数可以决定多个姓名和课号,因为一个学生选修一门课考完试当然只有一个成绩啦,一个分数能够有很多人考到,比如100分就特别多(干巴爹!你就是其中一个!),因此学号和课号二者跟分数是多对一的关系,因此可以得出,(sno,cno)→grade
so懂了叭还不懂偶也莫得了xddd
非平凡函数依赖:
符号表示:X→Y,Y⊊X
定义:当关系中属性集合Y不是属性集合X的子集时,存在函数依赖自X→Y,则称这种函数依赖为非平凡函数依赖。
理解定义:理解了函数依赖就好理解这个了,X决定Y,而Y不是X的子集。
实例:选择题:在关系SC(Sno,Cno,Grade)中,非平凡函数依赖包括()。
A.(Sno,Cno)→Sno
B.(Sno,Cno)→Cno
C.(Sno,Cno)→Grade
D.(Sno,Grade)→Cno
先看AB,虽然AB的依赖关系都是正确的,但是A中Sno作为Y,(Sno,Cno)作为X,Sno存在(Sno,Cno)中,也就是X→Y,Y⊆X,因此属于平凡函数依赖,B同理~,C的依赖关系也是正确的,还不懂咋判断依赖关系往上看哇233,Grade也不在(Sno,Cno)中,所以有X→Y,Y⊊X,故选C,再看D,一个学号和一个分数可以决定多个课号,一门课号可以决定多个学号和分数,比如偶的数据结构考了80分,会计学基础考了80分(滑稽,好吧严肃点把会计学当然程序设计语言吧,毕竟偶只是计算机专业),数据结构可以有很多名学生的考试成绩,因此,(Sno,Grade)与Cno是多对多的关系,不存在依赖关系,本身式子纠错啦233
平凡函数依赖:
定义:X→Y,但Y⊆x,则称X→Y是平凡的函数依赖。对于任一 关系模式,平凡函数依赖
都是必然成立的,它不反映新的语义。若不特别声明,总是讨论非平凡的函数依赖。
偷懒:这里就不一一理解啦,跟非平凡依赖差不多相反的啦der~~
完全函数依赖:
书上讲得好哇哈哈哈哈哈

部分函数依赖:
讲得好哇蛤蛤哈

完全函数依赖和部分函数依赖的判断:
对于表Student(sno,cno,Grade,Sdept),默认分数和系别在表中允许存在相同的值,学号和课程号都不允许存在相同的值。

(字丑该挨打
传递函数依赖:
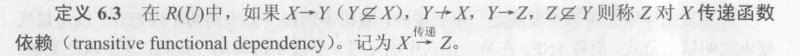
对于表Student(sno,cno,Grade,Sdept),默认分数和系别在表中允许存在相同的值,学号和课程号都不允许存在相同的值。

