1、10001的补码是取反后在再加1,也就是11110+1=11111;
2、如果是11111变回原码呢?我们可以采取逆过程先减1,11111-1=11110,再取反变为10001;
3、如果要是在补码变原码时先去反再加一呢?(就是问题中的说法)结果为11111先取反为10000,再加1,10000+1=10001。这个结果与2是一样的,并且也是和1中的原码相吻合。
在取反前减1和在取反后加1的效果是一样的。这就和-3-1=-(3+1)是一个道理。
计算机保存最原始的数字,也是没有正和负的数字,叫没符号数字
如果我们在内存分配4位(bit)去存放无符号数字,是下面这样子的


后来在生活中为了表示“欠别人钱”这个概念,就从无符号数中,划分出了“正数”和“负数”
正如上帝一挥手,从混沌中划分了“白天”与“黑夜”
为了表示正与负,人们发明了”原码”,把生活应该有的正负概念,原原本本的表示出来
把左边第一位腾出位置,存放符号,正用0来表示,负用1来表示


但使用“原码”储存的方式,方便了看的人类,却苦了计算机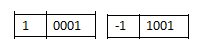
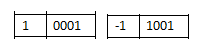
我们希望 (+1)和(-1)相加是0,但计算机只能算出0001+1001=1010 (-2)
这不是我们想要的结果 (╯’ – ‘)╯︵ ┻━┻
另外一个问题,这里有一个(+0)和(-0)
为了解决“正负相加等于0”的问题,在“原码”的基础上,人们发明了“反码”
“反码”表示方式是用来处理负数的,符号位置不变,其余位置相反


当“原码”变成“反码”时,完美的解决了“正负相加等于0”的问题
过去的(+1)和(-1)相加,变成了0001+1101=1111,刚好反码表示方式中,1111象征-0
人们总是进益求精,历史遗留下来的问题—— 有两个零存在,+0 和 -0
我们希望只有一个0,所以发明了”补码”,同样是针对”负数”做处理的
“补码”的意思是,从原来”反码”的基础上,补充一个新的代码,(+1)
我们的目标是,没有蛀牙(-0)

 有得必有失,在补一位1的时候,要丢掉最高位
有得必有失,在补一位1的时候,要丢掉最高位
我们要处理”反码”中的”-0″,当1111再补上一个1之后,变成了10000,丢掉最高位就是0000,刚好和左边正数的0,完美融合掉了
这样就解决了+0和-0同时存在的问题
另外”正负数相加等于0″的问题,同样得到满足
举例,3和(-3)相加,0011 + 1101 =10000,丢掉最高位,就是0000(0)
同样有失必有得,我们失去了(-0) , 收获了(-8)
以上就是”补码”的存在方式
结论:保存正负数,不断改进方案后,选择了最好的”补码”方案
二进制数在内存中以补码的形式存储。
按位取反:二进制每一位取反,0变1,1变0。
| ~9的计算步骤: 转二进制:0 1001 计算补码:0 1001 按位取反:1 0110 _____ 转为原码:
|
| ~-9的计算步骤: 转二进制:1 1001 计算补码:1 0111 按位取反:0 1000 _____ 转为原码:
|
原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。例如,用8位二进制表示一个数,+11的原码为00001011,-11的原码就是10001011。
反码表示法规定:正数的反码与其原码相同;负数的反码是对其原码逐位取反,但符号位除外。
补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
(1) 原码:在数值前直接加一符号位的表示法。
[+7]原= 0 0000111 B
[-7]原= 1 0000111 B
注意:
a. 数0的原码有两种形式:
[+0]原=0 0000000 B
[-0]原=1 0000000 B
b. 8位二进制原码的表示范围:-127~+127
(2)反码:
正数:正数的反码与原码相同。
负数:负数的反码,符号位为“1”,数值部分按位取反。
[+7]反= 0 0000111 B
[-7]反= 1 1111000 B
注意:
a. 数0的反码也有两种形式,即
[+0]反=0 0000000 B
[-0]反=1 1111111 B
b. 8位二进制反码的表示范围:-127~+127
(3)补码
正数:正数的补码和原码相同。
负数:负数的补码则是符号位为“1”。并且,这个“1”既是符号位,也是数值位。数值部分按位取反后再在末位(最低位)加1。也就是“反码+1”。
| 求负整数的补码,原码符号位不变,先将原码减去1,最后数值各位取反。(但由于2进制的特殊性,通常先使数值位各位取反,最后整个数加1。) |
例如: 符号位 数值位
[+7]补= 0 0000111 B
[-7]补= 1 1111001 B
| 注意: a. 采用补码后,可以方便地将减法运算转化成加法运算,运算过程得到简化。正数的补码即是它所表示的数的真值,而负数的补码的数值部份却不是它所表示的数的真值。采用补码进行运算,所得结果仍为补码。 b. 与原码、反码不同,数值0的补码只有一个,即 [0]补=00000000B。 c. 若字长为8位,则补码所表示的范围为-128~+127;进行补码运算时,应注意所得结果不应超过补码所能表示数的范围。 |
转化为原码已知一个数的补码,求原码的操作其实就是对该补码再求补码: |
大多数语言都提供了按位运算符,恰当的使用按位运算符有时候会取得的很好的效果。
在我看来按位运算符应该有7个:
1、& 按位与
&是二元运算符,它以特定的方式的方式组合操作数中对应的位,如果对应的位都为1,那么结果就是1, 如果任意一个位是0 则结果就是0。
1 & 3的结果为1
那我们来看看他是怎么运行的
1的二进制表示为 0 0 0 0 0 0 1
3的二进制表示为 0 0 0 0 0 1 1
根据 & 的规则 得到的结果为 0 0 0 0 0 0 0 1,十进制表示就是1
2、| 按位或
|运算符跟&的区别在于如果对应的位中任一个操作数为1 那么结果就是1。
1的二进制表示为 0 0 0 0 0 0 1
3的二进制表示为 0 0 0 0 0 1 1
所以 1 | 3的结果为3
3、^ 按位异或
^运算符跟|类似,但有一点不同的是 如果两个操作位都为1的话,结果产生0。
1的二进制表示为 0 0 0 0 0 0 1
3的二进制表示为 0 0 0 0 0 1 1
所以 1 ^ 3的结果为2
4、~ 按位非
~运算符是对位求反,1变0,0变1,也就是求二进制的反码
1的二进制表示为 0 0 0 0 0 0 1
所以 ~1 的结果是-2
5、>> 右移
>>运算符使指定值的二进制所有位都右移规定的次数,对于其移动规则只需记住符号位不变,左边补上符号位即按二进制形式把所有的数字向右移动对应的位数,低位移出(舍弃),高位的空位补符号位,即正数补零,负数补1。
1的二进制表示为 0 0 0 0 0 0 1
所以 1>>1的结果为0
6、<< 左移
<<运算符使指定值的二进制所有位都左移规定的次数,对于其移动规则只需记住丢弃最高位,0补最低位即按二进制形式把所有的数字向左移动对应的位数,高位移出(舍弃),低位的空位补零。
1的二进制表示为 0 0 0 0 0 0 1
所以 1<<1的结果为2 7、>>> 无符号右移
>>>运算符忽略了符号位扩展,0补最高位,但是只是对32位和64位的值有意义。
位运算符在js中的妙用:
1、使用&运算符判断一个数的奇偶
偶数 & 1 = 0
奇数 & 1 = 1
那么0&1=0,1&1=1
2、使用~~,>>,<<,>>>,|来取整
~~3.14 = 3
3.14 >> 0 = 3
3.14 << 0 = 3 3.14 | 0 = 3 3.14 >>> 0 = 3(>>>不可对负数取整)
注意:~~-3.14 = -3 其它的一样
3、使用<<,>>来计算乘除
乘法:
1*2 = 2
1<>1 = 1(2/2的一次方)
4、利用^来完成比较两个数是否相等
1 ^ 1 = 0
1 ^ 非1数 !=0
所以同一个数……同一个数等于0,否则不等于0
5、使用^来完成值交换
a = 1
b = 2
a ^= b
b ^= a
a ^= b
结果a=2,b=1
6、使用&,>>,|来完成rgb值和16进制颜色值之间的转换
16进制颜色值转RGB:
1 function hexToRGB(hex){ 2 var hex = hex.replace("#","0x"), 3 r = hex >> 16, 4 g = hex >> 8 & 0xff, 5 b = hex & 0xff; 6 return "rgb("+r+","+g+","+b+")"; 7 }
RGB转16进制颜色值:
1 function RGBToHex(rgb){ 2 var rgbArr = rgb.split(/[^d]+/), 3 color = rgbArr[1]<<16 | rgbArr[2]<<8 | rgbArr[3]; 4 return "#"+color.toString(16); 5 }
运行hexToRGB(“#ffffff”)返回”rgb(255,255,255)”
运行RGBToHex(“rgb(255,255,255)”)返回”#ffffff”
~ 运算符查看表达式的二进制表示形式的值,并执行位非运算。
Javascript 按位取反运算符 (~) ,对一个表达式执行位非(求非)运算。如 ~1 = -2; ~2 = -3;
js取反我只知道个!,但是~为什么也叫取反,他返回的又不是boolean类型?
~1,~2 的二进制又不是 -2 ,-3 ,怎么会转换成这么奇怪的值?
网友解答:
按位取反还真和boolean没多大关系,大体流程是这样的:
就来看看~1的计算步骤:
将1(这里叫:原码)转二进制 = 00000001
按位取反 = 11111110
发现符号位(即最高位)为1(表示负数),将除符号位之外的其他数字取反 = 10000001
末位加1取其补码 = 10000010
转换回十进制 = -2
有网友对上面的答案进行了三点补充,如下:
按位取反的运算规则这么奇怪并不是JavaScript独有的,而是所有的计算机语言都是这样的。这样做的主要原因是为了为了统一减法和加法,在计算机中,减法会变成加一个负数,而负数会以补码的形式存储。而这样主要是因为补码和数字的十进制数有这么转换关系,负数:补码(x) = -x - 1,正数:补码(x) = x
因为补码是针对负数存在的,那么只要数据类型有无符号数,就没有这样的烦恼了,比如C语言有无符号整型,就能对无符号整型直接按位取反。
如果没有无符号类型,而且也只是想要按位取反,而不是附带补码的按位取反,需要另外的方法。让全1的数据和当前数据做按位抑或就行了。比如,你有一个32位的数据a,需要对它做按位取反,那么这样就行了:0xFFFF ^ a
