
§6 抛物面
例 :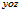 面上抛物线
面上抛物线 绕
绕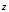 轴旋转,所得旋转面为
轴旋转,所得旋转面为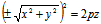 ,即
,即 
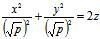 。
。
此曲面称为旋转抛物面,将该曲面推广便有:
一 椭圆抛物面:
1、定义:在直角系下,由方程 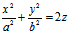 (a,b>0) (1)所表示的图形称为椭圆抛物面;而(1)称为椭圆抛物面的标准方程。
(a,b>0) (1)所表示的图形称为椭圆抛物面;而(1)称为椭圆抛物面的标准方程。
注:在直角系下,由方程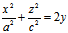 或
或 所表示的图形也是椭圆抛物面。
所表示的图形也是椭圆抛物面。
2、性质和形状:
(i)对称性:椭圆抛物面(1)关于z轴, 面,
面, 面对称,在ch6中,我们将会知道椭圆抛物面无对称中心。
面对称,在ch6中,我们将会知道椭圆抛物面无对称中心。
(ii)有界性:由(1)知z=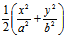 ≧0,∴椭圆抛物面(1)位于
≧0,∴椭圆抛物面(1)位于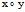 面的上方,且为无界的。
面的上方,且为无界的。
(iii)与坐标轴的交点及与坐标面的交线
(1)与三坐标轴均交于原点——顶点; (1)与三坐标面交于
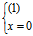 ,
, ,
,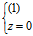 ,亦即
,亦即
 (2),
(2),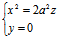 (3),
(3),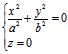 (4)
(4)
(2),(3)均为抛物线,其顶点均为原点,其开口方向均指z轴正向。对称轴均为z轴;而(4)为原点。
(iv)与平行于坐标面平面的交线:
首先,(1)与平行于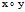 面的平面交于
面的平面交于 ,即
,即
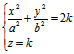 (
( ) (5)
) (5)
当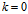 时,(5)为原点;
时,(5)为原点;
当 时,(5)为椭圆,其顶点为(0,±b
时,(5)为椭圆,其顶点为(0,±b ,k)∈(2), (±a
,k)∈(2), (±a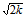 ,0,k)∈(3).
,0,k)∈(3).
可见,椭圆抛物面(1)是由 面上方的一系列”平行”椭圆构成,这些椭圆的顶点在抛物线(2)和(3)上变化。
面上方的一系列”平行”椭圆构成,这些椭圆的顶点在抛物线(2)和(3)上变化。
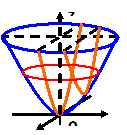

(图4.6)
另外,椭圆抛物面(1)与平行于 面的平面交于
面的平面交于 ,即
,即
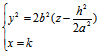 (6)
(6)
对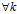 ,(6)均为全等的抛物线,其顶点(
,(6)均为全等的抛物线,其顶点( ,0,
,0,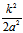 )∈(3)对称轴∥z轴,开口方向朝z轴正向(与(3)的开口方向一致)
)∈(3)对称轴∥z轴,开口方向朝z轴正向(与(3)的开口方向一致)
最后,若用平行于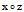 面的平面去截(1),其截线情况于上类似,由此可得椭圆抛物面的几何特征如下:
面的平面去截(1),其截线情况于上类似,由此可得椭圆抛物面的几何特征如下:
椭圆抛物面是由一抛物线沿另一定抛物线移动而形成的轨迹,在移动过程中,动抛物线的顶点始终在定抛物线上,开口方向与定抛物线开口方向一致,且它们所在平面始终保持垂直(如图4.6)。
二 双曲抛物面:
1、定义:在直角系下,由方程 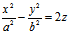 (a,b>0) (1)所表示的图形称为双曲抛物面;而(1)称为双曲抛物面的标准方程。
(a,b>0) (1)所表示的图形称为双曲抛物面;而(1)称为双曲抛物面的标准方程。
注:在直角系下,由方程 或
或 所表示的图形也是双曲抛物面。
所表示的图形也是双曲抛物面。
2、性质和形状:
(i)对称性:双曲抛物面(1)关于z轴,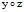 面,
面, 面对称,在ch6中,我们将会知道双曲抛物面无对称中心。
面对称,在ch6中,我们将会知道双曲抛物面无对称中心。
(ii)有界性:由(1)知双曲抛物面(1)为无界的。
(iii)与坐标轴的交点及与坐标面的交线
(1)与三坐标轴均交于原点——顶点; (1)与三坐标面交于
 ,
, ,
, ,亦即
,亦即
 (2),
(2),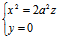 (3),
(3),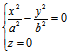 (4)
(4)
(2),(3)均为抛物线,其顶点均为原点,其开口方向一指z轴正向,一朝z轴负向。对称轴均为z轴;而(4)为二相交直线。
(iv)与平行于坐标面平面的交线:
首先,(1)与平行于 面的平面交于
面的平面交于 ,即
,即
 (5)
(5)
当 时,(5)为(4);
时,(5)为(4);
当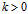 时,(5)为双曲线,其顶点为(±a
时,(5)为双曲线,其顶点为(±a ,0,k)∈(3).
,0,k)∈(3).
当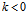 时,(5)仍为双曲线,其顶点为(0,±
时,(5)仍为双曲线,其顶点为(0,±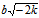 , k)∈(2)
, k)∈(2)
可见,双曲抛物面(1)是平行于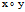 面的一系列”平行”双曲线构成,这些双曲线的顶点在抛物线(2)和(3)上变化。
面的一系列”平行”双曲线构成,这些双曲线的顶点在抛物线(2)和(3)上变化。
另外,双曲抛物面(1)与平行于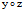 面的平面交于
面的平面交于 ,即
,即
 (6)
(6)
对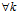 ,(6)均为全等的抛物线,其顶点(k,0,
,(6)均为全等的抛物线,其顶点(k,0, )∈(3)对称轴∥z轴,开口方向朝z轴负向(与(3)的开口方向相反)
)∈(3)对称轴∥z轴,开口方向朝z轴负向(与(3)的开口方向相反)
最后,若用平行于 面的平面去截(1),其截线情况于上类似,由此可得双曲抛物面的几何特征如下:
面的平面去截(1),其截线情况于上类似,由此可得双曲抛物面的几何特征如下:
双曲抛物面是由一抛物线沿另一定抛物线移动而形成的轨迹,在移动过程中,动抛物线的顶点始终在定抛物线上,开口方向与定抛物线开口方向相反,且它们所在平面始终保持垂直(如图4.7)。


(图4.7)

欢迎访问我的专业知识博客!
博主:白途思(begtostudy)
微信/QQ:370566617
Email:begtostudy#gmail.com
欢迎访问我的其他博客:我的编程知识博客 我的学术知识博客
