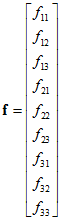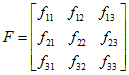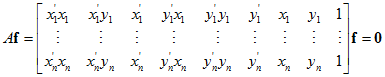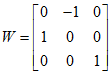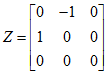本质矩阵E求解及运动状态恢复

为了获取本质矩阵，首先计算基础矩阵F。根据本质矩阵E，即可恢复得到运动的状态R和T。

由可以根据匹配点得到F，然后根据和相机内参，即可得到本质矩阵E。进而根据：

注意：根据摄像机模型t=-RT，恢复运动状态，就是要计算t和R。

8点法

8点算法是计算基本矩阵的最简单的方法，它涉及构造并（最小二乘）解一个线性方程组。给定足够多的匹配点（至少7对），可解得基础矩阵F。

记和，每一组点匹配提供关于的未知元素的一个线性方程。对应于一对点和的方程是：

写成矩阵（矢量）的形式：

其中：

 

从而根据n对匹配的点集，我们可以得到线性方程组：

计算最小二乘解，的最小二乘解是对应于的最小奇异矩阵的奇异矢量，即是的SVD分解中矩阵的最后一列矢量。用这种方法得到的解矢量在条件下取的最小值。

该方法步骤简单，易于实现，但由于其计算结果对输入数据异常敏感，从而直接影响它在实际中的应用。

1997年，Hartley对原始8点算法进行改进，在构造解的方程之前对输入的数据进行适当的归一化。即在形成8点算法的线性方程组之前，图像点的一个简单变换（平移或变尺度）将使这个问题的条件极大地改善，从而提高结果的稳定性。而且进行这种变换所增加的计算复杂性并不显著。算法具体过程具体如下：

对原始图象坐标做一个平移变换，使原来以左上角为原点的图象坐标变成以所有图像点的重心为原点的图像坐标；
再对图象坐标做一个尺度变换，使得点到原点的平均距离为。

分别对两幅图像进行以上两步变换，然后将变换后的图像坐标作为输入数据计算基础矩阵。

计算过程如下：

设两个独立的图像坐标变换分别为T、，则变换后的图像坐标为和；
基于转换后的匹配点对，利用八点算法计算基础矩阵；
解除归一化，令，矩阵F是对应于原始数据的基本矩阵。

注意：此时求得的F阵的秩并不保证严格为2。而且，由于噪声影响计算得到的F一般都是满秩的。

进而，根据相机的内参信息得到本质矩阵E。

运动恢复

在二视图中，第一个相机的投影矩阵为：，而第二个相机的投影矩阵为：，投影矩阵的旋转矩阵R和平移矩阵t是要被计算出来的，计算的过程称为运动恢复。这里的“运动”就是第二帧相机相对于第一帧相机的运动变化。

1992年，Hartley提出了从本质矩阵在相差一个尺度因子的情况下恢复出摄像机投影矩阵的四个可能解，然后从四个解中选择一个正确解的方法。证明过程可见“计算机视觉中的多视图几何”中文本174页。

定理1：一个3*3的矩阵是本质矩阵的充要条件是它的奇异值中有两个相等而第三个是0。

定理2：设本质矩阵的SVD分解是：，不考虑本质矩阵的符号，则存在两种可能的解：

,

,

其中：

 

推论：已知本质矩阵和第一和摄像机矩阵，那么第二个摄像机矩阵有下列四种可能的选择：

是的最后一列。

t的具体空间长度是不能恢复出来的，只能在相差一个尺度因子的情况下恢复平移单位向量。

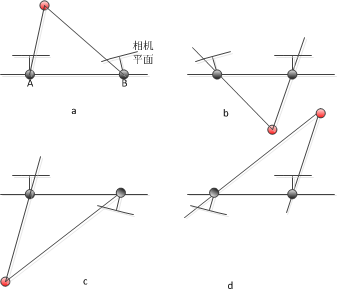
4个解的几何解释

显然前面两个解的差别就是第一个摄像机到第二个摄像机的平移矢量是反向的。

上下两行的差别在于摄像机绕基线旋转了180度，上图中只有（a）时，重构点同时出现在两个摄像机的前面。

从匹配点对中随机选择n对特征点，采用视图重建的方法，分别基于四种可能的摄像机矩阵重建出对应的三维点，满足景深为正的点数最多的解就是对应的,同时也可以确定相机的外参R和t。