1、什么是流形
流形学习的观点:认为我们所能观察到的数据实际上是由一个低维流行映射到高维空间的。由于数据内部特征的限制,一些高维中的数据会产生维度上的冗余,实际上这些数据只要比较低的维度就能唯一的表示。所以直观上来讲,一个流形好比是一个$d$维的空间,在一个$m$维的空间中$(m > d)$被扭曲之后的结果。需要注意的是流形并不是一个形状,而是一个空间。举个例子来说,比如说一块布,可以把它看成一个二维的平面,这是一个二维的空间,现在我们把它扭一扭(三维空间),它就变成了一个流形,当然不扭的时候,它也是一个流形,欧式空间是流形的一种特殊情况。如下图所示
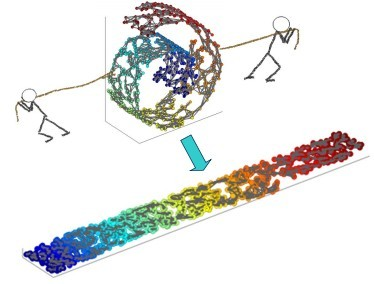
再比如对于一个球面上的一点(其实就是三维欧式空间上的点),可以用一个三元组来表示其坐标:
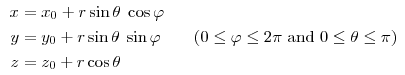
但事实上这三维的坐标只由两个变量$ heta$和$varphi$生成的,也可以说成是它的自由度是2,也正好对应了它是一个二维的流形。
流形具有在局部与欧式空间同胚的空间,也就是它在局部具有欧式空间的性质,能用欧式距离来进行距离计算。这就给降维带来了很大的启发,若低维流形嵌入到了高维空间,此时样本在高维空间的分布虽然复杂,但在局部上仍具有欧式空间的性质,因此可以在局部建立降维映射关系,然后再设法将局部映射关系推广到全局。而且当数据被降维到二维和三维时,就可以进行可视化,因此流形学习也可以被用于可视化。
2、等度量映射(Isomap)
首先介绍下MDS算法,MDS算法的核心思想:找到一个低维空间使得样本间的距离在高维空间和低维空间基本一致。所以MDS算法是利用样本间的相似性来保持降维后的输出结果与降维前一致(此种算法的计算量很大),然而对于高维空间直接计算样本之间的直线距离(欧式距离)是具有很大的误导性的。举个例子,计算地球上南极到北极之间的距离,可以直接计算这两点之间的距离,但是这种距离是毫无意义的(你总不能从南极打个洞到北极吧),因此引入了测地距离,测地距离才是两点之间的本真距离。具体如下如所示
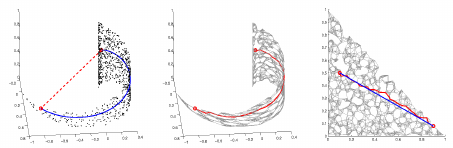
然而如何计算两点之间的测地距离呢,毕竟从南极到北极有很多条路径,不过我们要求的是从南极到北极之间的最短的测地距离。这时就可以利用流形在局部上与欧式空间同胚这个性质,对于每个点基于欧式距离找出其最近邻点,然后就能建立一个近邻连接图,于是计算两点之间的测地距离的问题,就转变成为计算近邻连接图上两点之间的最短路径问题(Dijkstra算法)。
那么什么是Isomap算法呢?其实就是MDS算法的变种,其思想和MDS一样,只不过在计算高维空间的距离时是采用测地距离的,而不是无法真实的表达两点之间的欧式距离。具体算法流程如下(来源:机器学习周志华版)

Isomap算法是全局的,它要找到所有样本全局的最优解,当数据量很大时或者样本维度很高时,计算量非常大。因此更常用的算法是LLE(局部线性嵌入),LLE放弃所有样本全局最优的降维,只是通过保证局部最优来降维。
3、局部线性嵌入(LLE)
局部线性嵌入的思想:只是试图去保持领域内样本之间的关系。具体如下图所示,样本从高维空间映射到低维空间后,各个领域内的样本之间的线性关系不变。
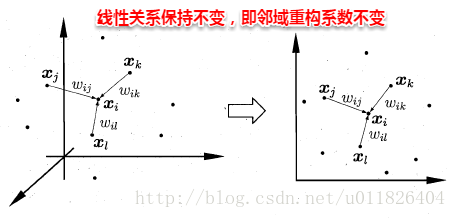
即样本点$x_i$的坐标能通过它的领域样本$x_j, x_l, x_k$重构出来,而这里的权值参数在低维和高维空间是一致的。
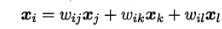
LLE算法可以分为两步:
第一步根据邻域关系计算出所有的样本的领域重构系数$w$,也就是找出每一个样本和其领域内的样本之间的线性关系

第二步就是根据领域重构系数不变,去求每个样本在低维空间的坐标
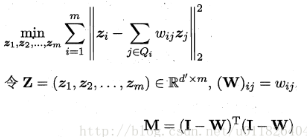
利用M矩阵,可以将问题写成

因此问题就成了对$M$矩阵进行特征分解,然后取最小的$d’$个特征值对应的特征向量组成低维空间的坐标$Z$。LLE算法具体的流程如下(来源:机器学习周志华版)

LLE算法总结:
主要优点:
1)可以学习任意维的局部线性的低维流形。
2)算法归结为稀疏矩阵特征分解,计算复杂度相对较小,实现容易。
3)可以处理非线性的数据,能进行非线性降维。
主要缺点:
1)算法所学习的流形只能是不闭合的,且样本集是稠密的。
2)算法对最近邻样本数的选择敏感,不同的最近邻数对最后的降维结果有很大影响。
