协方差矩阵计算方法

1. 协方差定义

X、Y 是两个随机变量，X、Y 的协方差 cov(X, Y) 定义为：

其中：

 、

2. 协方差矩阵定义
矩阵中的数据按行排列与按列排列求出的协方差矩阵是不同的，这里默认数据是按行排列。即每一行是一个observation(or sample)，那么每一列就是一个随机变量。

n个随机变量，m个样本。

协方差矩阵：

协方差矩阵的维度等于随机变量的个数，即每一个 observation 的维度。在某些场合前边也会出现 1 / m，而不是 1 / (m – 1).

3. 求解协方差矩阵的步骤

举个例子，矩阵 X 样本按行排列：

 

 

1. 求每个维度的平均值

 

 

2. 将 X 的每一列减去平均值

 

 
其中：

 

3. 计算协方差矩阵

 

4. MATLAB 示例

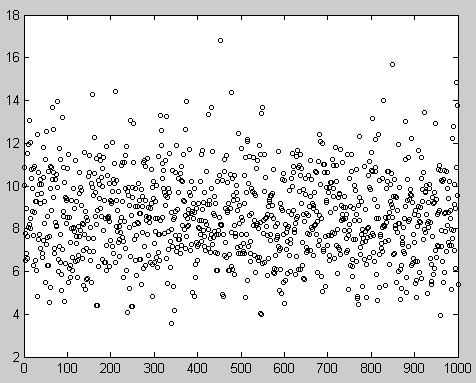
data = randn(1000, 10); 
n = length(data); % 样本数目
mu = mean(data, 1); % 均值行向量
MU = repmat(mu, n, 1); % 均值矩阵（重复n次，变为n行1列的均值矩阵）
s = (data-MU)'*(data-MU)/(124-1); % 协方差矩阵

% 计算马氏距离
DM = zeros(n, 1);
for i = 1:n
    xi = data(i, :);
    DMi = sqrt((xi'-mu')'*s*(xi'-mu'));
    DM(i) = DMi;
end

plot(DM, 'ko', 'markersize', 3)