
在计算机体系中,数据并行有两种实现路径:MIMD(Multiple Instruction Multiple Data,多指令流多数据流)和SIMD(Single Instruction Multiple Data,单指令流多数据流)。其中MIMD的表现形式主要有多发射、多线程、多核心,在当代设计的以处理能力为目标驱动的处理器中,均能看到它们的身影。同时,随着多媒体、大数据、人工智能等应用的兴起,为处理器赋予SIMD处理能力变得愈发重要,因为这些应用存在大量细粒度、同质、独立的数据操作,而SIMD天生就适合处理这些操作。
SIMD结构有三种变体:向量体系结构、多媒体SIMD指令集扩展和图形处理单元。本文集中围绕向量体系结构进行描述。
向量体系结构的基本组成
1.简介
向量体系结构使用一条向量指令开启一组数据操作,其中数据的加载、存储以及数据计算以流水线的形式进行。它最大的特点就是:其仅在一组数据操作的第一个元素存在存储器延迟和由冒险引起的停顿,后续元素会沿着流水线顺畅流动。
我们通过一个以cray-1为基础的向量处理器来分析。它同时包含标量体系结构和向量体系结构,其标量指令集为MIPS,向量指令集则称为VMIPS。
2.架构组成
VMIPS指令集体系结构的主要组件如下图所示:
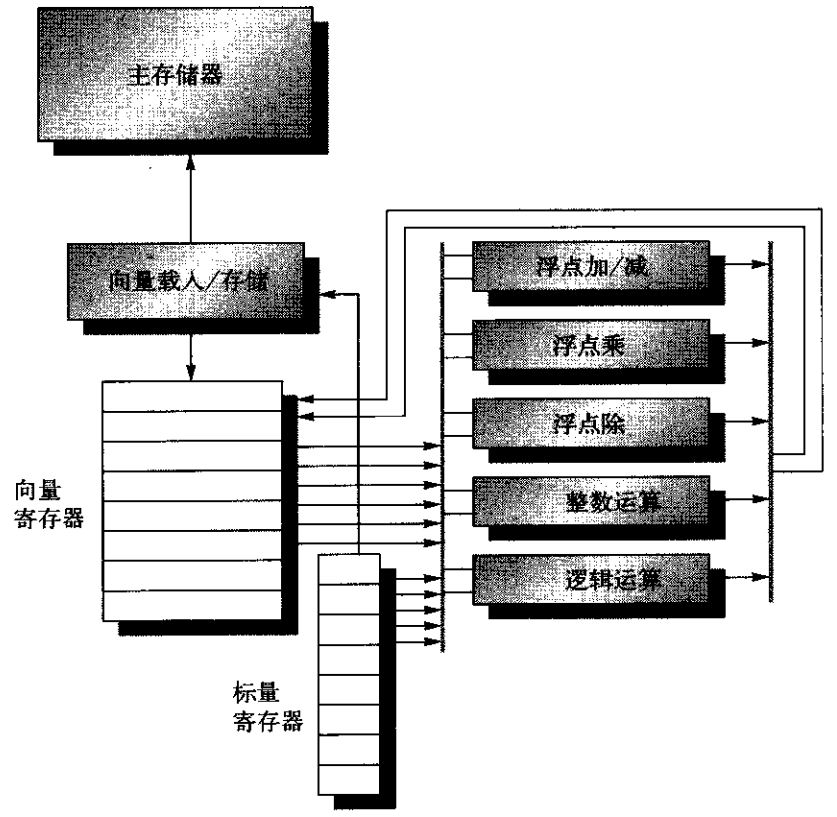
图1 向量体系结构VMIPS的基本结构
向量寄存器:N个向量寄存器,每个向量寄存器都是一个固定长度的寄存器组,用于保存一个向量。向量长度通常为32、64等,这也是单条向量指令所能执行元素的最大值。
标量寄存器:用于给向量功能单元提供标量输入数据、给载入/存储单元提供地址,或是作为向量长度寄存器、向量遮罩寄存器等功能。
向量功能单元:每个单元都完全实现流水化,可以在每个时钟周期开启一个新的操作。每个功能单元可能只有单条流水线(单车道),也可以有多个并行的流水线(多车道)。
向量载入/存储单元:向量载入与存储操作也是完全流水化的,在初始延迟后,可以以每个时钟周期一个只的带宽移动字。该单元通常还会处理标量载入和存储。
3.向量长度寄存器
向量处理器有一个自然向量长度,由向量寄存器的长度决定。然而在实际程序中,特定向量运算的长度在编译时通常是未知的。例如以下代码:
for (i=0; i<n; i++)
{
y[i] = a * x[i] + y[i];
}
向量运算的长度取决于n,而n是个变量,它可能在执行时随应用情况而变化。
向量长度寄存器(VLR)就是为了解决实际数据向量长度变化这一问题,它控制一条向量指令执行元素的长度,但这一长度不能超过自然向量长度。
4.向量遮罩寄存器
考虑如下循环:
for (i=0; i<64; i++)
{
if (y[i] != 0)
{
y[i] = x[i] – y[i];
}
}
由于循环体需要条件执行,因此不可能对一组数据向量的元素执行相同操作,也就不便于对循环进行向量化。
通过启用向量遮罩寄存器可以解决这一问题。它可以通过布尔向量来控制一条向量指令中每个元素运算的条件执行,如向量中某元素对应的向量遮罩寄存器中的布尔值为1,则执行指令操作,否则执行空操作。
需要注意的一点是,即使遮罩为0的元素,它仍会占用与遮罩为1元素相同的执行时间。
较标量处理器的优势
向量体系结构与标量体系结构相比,其优势有:
仅在每个向量载入或存储操作中付出较长的存储器延迟时间,而不需要在载入或存储每个元素时耗费时间。
减少了流水线互锁的频率。多个指令间可能由于相关性而引起停顿,向量体系结构中每条向量指令仅需一次流水线停顿,而不是每个向量元素操作需要一次。
大幅缩减了动态指令带宽。向量体系结构使原本在标量体系中每个元素操作需要一条指令,变成了每个向量操作仅需要一条向量指令。
向量体系结构 & 软件流水线
在看向量体系结构的指令处理过程时,很容易将它与软件流水线的概念混淆在一起。实际上二者确实有很多相似之处,我们可以通过一个例子来分析:
for(i=0 ; i<16; i++)
{
sum += tab[i];
}
如上的一个循环体,实现16长度的数组求和。假设处理器中含有并行的加载/存储单元(.D)与算术单元(.L),.D单元执行一条指令消耗4个时钟周期,.L单元执行一条指令消耗1个时钟周期。
在标量处理器中不进行软件流水线编排,假设不考虑循环操作指令的开销,其在不同时刻执行指令的过程大致如下所示:
clock .D .L
1 load1
2
3
4
5 load2 add1
6
7
8
9 load3 add2
……
61 load16 add15
62
63
64
65 add16 (结束)
在标量处理器中进行指令软件流水线编排后,在不同时刻执行指令的过程大致如下所示:
clock .D .L
1 load1
2 load2
3 load3
4 load4
5 load5 add1
6 load6 add2
7 load7 add3
8 load8 add4
10 load9 add5
11 load10 add6
12 load11 add7
13 load12 add8
14 load13 add9
15 load14 add10
16 load15 add11
17 load16 add12
18 add13
19 add14
20 add15
21 add16 (结束)
在向量处理器中,假设向量长度为16,功能单元仅有单车道,在不同时刻执行指令的过程大致如下所示:
clock .D .L
1 vload
2
3
4
5 vadd
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 (结束)
从以上的例子中可以很清楚地看出:
软件流水线和向量指令具有相同的时钟消耗,它们都仅在处理第一个元素时才发生延迟停顿。
软件流水线并没有减少指令的个数,而向量指令处理一组向量操作仅需一条向量指令。
总结起来就是:软件流水线可以减少流水线停顿,但很难大幅缩减指令带宽要求;而向量体系结构既能减少流水线停顿,也能大幅缩减指令带宽要求。
也有现代处理器专门针对软件流水线而设计硬件和指令支持。例如TI C6000架构中的SLOOP BUFFER单元和软件流水指令,可以将上述软件流水线例子中clock5~clock17的指令表示成一条load和add指令,称为软件流水核。这样的处理方式也实现了缩减指令带宽的目的。
因此,宏观上可以认为:向量体系结构是通过指令集的设计支持,在硬件上实现可向量化循环的流水化操作;软件流水线是通过编译器端的指令编排(或是加上部分硬件设计支持),在软件上实现可向量化循环的流水化操作。
一些现实问题
1.处理非整数倍自然向量长度的向量
在实际程序中,特定向量运算的长度通常都是未知的,比如以下代码:
for (i=0; i<n; i++)
{
y[i] = a * x[i] + y[i];
}
假设向量体系结构的自然向量长度MVL=64,当n=64k(1,2……),我们可以很方便的把代码写成一个向量指令的k次循环。但更有可能的是,n不为64的整数倍,为了应对各种不同的情况,该怎么组织代码呢?
一种名为条带挖掘(strip mining)的技术能解决这一问题。条带挖掘是指生成一些代码,使每个向量运算都是针对小于或等于MVL的大小来完成的。事实上任何n都可以差分成MVL的整数倍部分和余数部分,于是我们可以创建两个循环,分别处理这两个部分。向量体系结构利用向量长度寄存器,在编译时可以生成一个条带挖掘循环。
处理上面例子的条带挖掘C语言的写法如下:
low = 0;
VL = (n % MVL)
for(j=0; j<=(n/MVL); j++)
{
for(i=low; i<(low+VL); i++)
{
y[i] = a * x[i] + y[i];
}
low += VL;
VL = MVL;
}
如此便可将整个向量分段,第一段的长度为余数部分(n%MVL),后续段长度为MVL。
2.提供充足的内存带宽:内存组(memory bank)
以下几个原因造成向量处理器对存储带宽需求很大:
许多向量处理器单时钟周期可以产生多个内存访问操作
可能存在多个向量处理器同时独立访问同一存储器系统
存储器组的周期时间通常比处理器周期时间高几倍
多数向量处理器支持非连续数据字的访问
对于存储器组而言,通常同一时刻对同一存储器组只能有一个访问存在,上面这些因素使得处理器架构师需要设置大量的独立存储器组,以满足同一时刻对多个存储器组的访问。
3.非单位步幅存储访问
当要访问的一组向量数据在内存中的位置并不是连续的,称这时元素的访问为非单位步幅。现实中有很多这样的例子,例如对矩阵的访问:
for(i=0; i<m ; i++)
{
C[i] = 0;
for(j=0; j<n; j++)
{
C[i] += A[i][j] * B[j][i];
}
}
由于在C语言中行元素是依次排列的,因此对矩阵A的访问就是单位步幅的,而对矩阵B的访问是非单位步幅的(设j>1)。
向量处理器的主要优势之一就是能够访问非连续存储器位置,并对其进行调整,放到一个密集结构中。不过,为支持大于1的步幅,会使存储器系统变得复杂。引入非单位步幅后,就有可能频繁访问同一个组,引起存储器组冲突,从而使某个访问停顿。
举个存储器组冲突的例子:假定有16个存储器组,组繁忙时间为6个时钟周期,每个时钟周期以步幅deta访问存储器的一个字(4字节):
Bank | 1 | 2 | 3 |…
Address | 0 1 2 3 | 4 5 6 7 | 8 9 10 11 |…
Address | 64 65 66 67 | 68 69 70 71 | 72 73 74 75 |…
若deta=1,则永远不会发生存储器组冲突;若deta=4,则第一次访问将与第五次访问发生冲突……
在《计算机体系结构.量化方法研究》这本书中,作者给出了一个判断是否会产生存储器组冲突的公式,可能由于笔误发生了一点小错误,原书表达如下:
若满足以下条件,则会产生组冲突,从而产生停顿:
(组数/步幅与组数的最小公倍数) < 组繁忙时间
实际上用这个公式去套上面的例子,显然是讲不通的。一开始我以为是翻译错误,然后去看了英文原本,书上是这么写的:
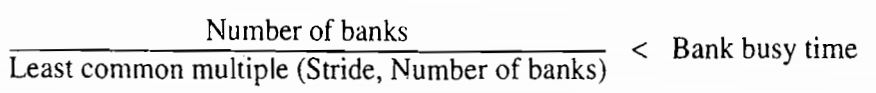
翻译并没有问题。我自己推导后,认为正确的表示应该是这样的:
若满足以下条件,则会产生组冲突,从而产生停顿:
(步幅与组数的最小公倍数/步幅) < 组繁忙时间
或者
(组数/步幅与组数的最小公约数) < 组繁忙时间
以下是推导过程,如有疏忽,请指正:

4.集中-分散存储访问
稀疏矩阵在应用中是很常见的,在稀疏矩阵中,向量的元素通常以某种紧凑形式存储,然后对其进行间接访问。我们可能会看到类似下面的代码:
for(i=0; i<n i++)
{
A[k[i]] = A[k[i]] + C[m[i]];
}
假设索引数组k和m的内容是不连续的,则对矩阵A和C的加载称为集中操作;对矩阵A的存储操作称为分散操作。对此类操作的支持被称为集中-分散(gather-scatter)。
几乎所有向量处理器都具备这一功能,这一技术允许以向量模式运行带有稀疏矩阵的代码。由于可能不知道k和m的值是离散的,简单的向量化编译器可能无法自动实现以上源码的向量化,需程序员给编译器发出提示。
参考资料
【1】John L. Hennessy,David A. Patterson . 计算机体系结构:量化研究方法:第5版[M].北京:人民邮电出版社,2013. (原名《Computer Architecture:A Quantitative Approach》)
·END·
欢迎来我的微信公众号做客:信号君
专注于信号处理知识、高性能计算、现代处理器&计算机体系
技术成长 | 读书笔记 | 认知升级

幸会~
![]()
你可能还感兴趣:
