条件随机场(CRF)
0. 预备知识
0.1 概率图模型(Probabilistic Graphical Model,PGM)
概念:图结构,结点(node)表示随机变量,边(edge)表示结点间关系。简而言之,不相连的结点直接毫无关系。
分类:
有向图:贝叶斯网络,变量之间的因果关系
无向图:马尔科夫随机场,变量之间的相关关系,常用于图像去噪等
0.2 团与极大团
定义:团就是一个两两之间有边的顶点集合
绿色圆圈是一个团,蓝色圆圈是一个极大团
0.3 势函数
概念:应用等势线、等高线的概念,存在一条等高线,使得高于等高线的属于(ψ_1),低于等高线的属于(ψ_2)
应用:node之间的相关关系通过势函数进行度量*(恒>=0,局部)
为了满足非负性,常用指数函数进行定义:
[ψ(x)=e^{-H(x)}\
其中H(x)是一个定义在变量x上的实值函数
]
对于一个x_{i}确定的区域,其势函数的表达式为 一个势函数有以下特点:
当X越接近时,
的函数值越大,当
时,
取得最大值
当X越远离时,
的函数值越小,特别的
(其中j不等于i)时,
值通常非常小
分类:
第一类势函数:采用对称的多项式展开,通常需要为正交函数集
第二类势函数:选择双变量的对称函数
当
时有最大值1 当x远离
时,趋近于0
0.4 马尔科夫性
马尔可夫随机场是生成式模型,生成式模型最关心的是变量的联合概率分布。
时间复杂度限制:
非相对独立时:n个取值的随机变量((x_1,x_2,…,x_n)),其取值分布包括(2^n)种可能,因此联合概率分布(p(x_1,x_2,…,x_n))需要(2_n-1)个参数
相对独立时:(p(x_1,x_2,…,x_n)) = (p(x_1)p(x_2)…p(x_n)),需要n个参数
能不能将联合概率分布分解为一组子集概率分布的乘积呢?那么应该怎么划分子图呢?应该遵循怎样的原则?
为确保条件独立
全局马尔科夫性:设节点集合A,B是在无向图G中被节点集C分开的任意节点集合,如下图所示。全局马尔可夫性是指在给定(x_C)的条件下,和(x_A)和(x_B)条件独立,记为((x_A⊥x_B)|x_C)
[p(x_A,x_B|x_C) = p(x_A|x_C)p(x_B|x_C)
]
局部马尔科夫性
[P(x_v,x_o|x_w) = p(x_v|x_w)p(x_o|x_w)
]
成对马尔科夫性
[p(x_i,x_j,x_{(i,j)}) = p(x_i|x_{(i,j)})p(x_j|x_{(i,j)})\
其中x_{(i,j)}表示所有变量x去除x_i和x_j的集合
]
0.5 马尔可夫随机场
我不清楚具体的定义,但我觉得满足马尔可夫性+随机场 = 马尔科夫随机场
在马尔可夫随机场中,多个变量的联合概率分布能基于团分解为多个势函数的乘积,每一个团对应一个势函数。马尔可夫随机场有一组势函数,亦称因子,这是定义在变量子集上的非负实函数,主要用于定义概率分布函数。
C是一个团,(ψ_C)为团C对应的势函数
[p(x) = frac{1}{Z}prod_C ψ_C(x_C)\
Z=sum_xprod_C ψ_C(x_C)
]
1. CRF介绍
1.1 CRF简介:
1.1.1 命名缘由:Conditional random field
Random指的是随机变量X和Y
Conditional指的是条件概率
1.1.2 CRF是在给定一组输入随机变量序列的条件下,输出目标序列
,且Y要是马尔科夫随机场
时序模型、判别模型
应用:词性标注
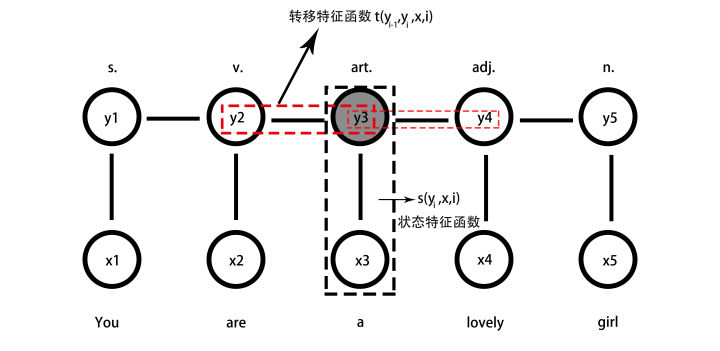
例子:词性标注
“Bob drank coffee at Starbucks”,注明每个单词的词性后是这样的:“Bob (名词) drank(动词) coffee(名词) at(介词) Starbucks(名词)”。
(名词,动词,名词,介词,名词)
(名词,动词,动词,介词,名词)
挑选出一个最靠谱的作为我们对这句话的标注
凡是标注中出现了动词后面还是动词的标注序列,要给它负分!!
上面所说的动词后面还是动词就是一个特征函数,我们可以定义一个特征函数集合,用这个特征函数集合来为一个标注序列打分,并据此选出最靠谱的标注序列。也就是说,每一个特征函数都可以用来为一个标注序列评分,把集合中所有特征函数对同一个标注序列的评分综合起来,就是这个标注序列最终的评分值。
输出值是0或者1,0表示要评分的标注序列不符合这个特征,1表示要评分的标注序列符合这个特征。

特征函数(f_j):
句子s(就是我们要标注词性的句子)
i,用来表示句子s中第i个单词
$ l_i$,表示要评分的标注序列第i个单词标注的词性
(l_{i-1}),表示要评分的标注序列给第i-1个单词标注的词性
(f_1(s,i,l_i,l_{i-1})=1) ,当(l_{i-1})是介词,(l_i)是名词时,(f_1 = 1),其他情况(f_1=0)。(λ_1)也应当是正的,并且(λ_1)越大,说明我们越认为介词后面应当跟一个名词。
将特征函数(f_j)赋予一个权重(λ_j),只有一个句子s,有一个标注序列 (l) ,对前面定义的特征函数集来对$ l $ 评分:
[score(l|s) = sum_{j=1}^msum_{i=1}^nlambda_jf_j(s,i,l_i,l_{i-1})
]
1.2 CRF参数化定义(书中是直接给定的,不懂)
CRF在统计语料库总相邻词是否满足特征函数的频次,给出(P_w(y|x))。在给定的((x,y)),满足的特征函数越多,模型认为(P_w(y|x))越大。
[p(x) = frac{1}{Z}prod_C ψ_C(x_C)\
Z=sum_xprod_C ψ_C(x_C)
]
softmax 随机神经网络 玻尔兹曼机
[P(y|x) = frac{1}{Z(x)}exp(sum_{i,k}lambda_kt_k(y_{i-1},y_i,x,i))+sum_{i,l}mu_ls_l(y_i,x,i))\
Z(x) = sum_yexp(sum_{i,k}lambda_kt_k(y_{i-1},y_i,x,i))+sum_{i,l}mu_ls_l(y_i,x,i))
]
每个(f_i)都有一个权重(omega),(t(y_{i-1},y_i,x,i)) 和 (s(y_i,x,i)) 用 (F(y,x)) 表示,将上式简化为:
[p_w(y|x) = frac{1}{Z_W(x)}exp(w*F(y,x))\
Z_w(x) = sum_yexp(w*F(y,x))
]
1.3 CRF到linear-CRF
1.3.1 数学定义
设 均为线性链表示的随机变量序列,在给定随机变量序列
的情况下,随机变量
的条件概率分布
构成条件随机场,即满足马尔科性:
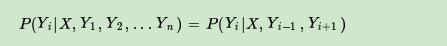
则称 为线性链条件随机场。
注意:
注意在CRF的定义中,我们并没有要求X和Y有相同的结构。而实现中,我们一般都假设
X和Y有相同的结构,即:
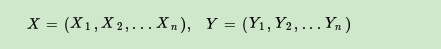
一般考虑如下图所示的结构:X和Y有相同的结构的CRF就构成了线性链条件随机场(Linear chain Conditional Random Fields,以下简称 linear-CRF)。
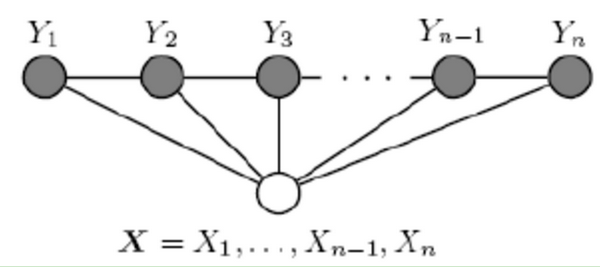
1.3.2 linear-CRF需要解决的三个问题:评估,学习和解码
2. Naive Bayes 、 Logistic Regression 、HMM 、 Linear-chain CRF
2.1 HMM vs CRF
每一个HMM模型都等价于某个CRF
有向 vs 无向
联合概率 vs 条件概率
CRF与逻辑回归的比较
事实上,条件随机场是逻辑回归的序列化版本。逻辑回归是用于分类的对数线性模型,条件随机场是用于序列化标注的对数线性模型。
https://zhuanlan.zhihu.com/p/29989121



