
1. 关于三角形边的不等式
关于三角形有一个常用的不等式,以下面的三角形为例:
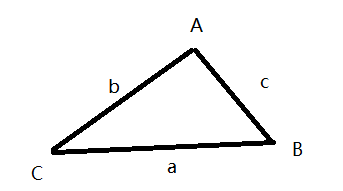
$$a + b > c \
a + c > b \
b + c > a$$
上面的三个不等式很容易理解,两点之间直线段最短,而两边之和相当于折线段,必然会小于直线段的长度。
上面三个不等式进行移项有
$$a > c – b \
a > b – c \
c > b – a \
c > a – b \
b > a – c \
b > c – a$$
所以
$$a > | b – c | \
c > | a – b | \
b > | a – c |$$
即任意两边之差小于第三边。
2. 向量三角不等式
这个不等式本质还是关于三角形三条边的关系,可以由 $1$ 推得,不等式内容如下
$$||a| – |b|| ; leq ; |a pm b| ; leq ; |a| + |b| $$
向量 $a + b$ 或者 $a – b$ 是由向量 $a$ 和向量 $b$ 构成的三角形的第三条边,而向量取绝对值(取模)之后就是向量长度(边长)。
所以上面的不等式本质就是三角形两边之和大于第三边,两边之差小于第三边。
3. 绝对值三角不等式
这个不等式很容易理解,其内容如下
$$||a| – |b|| ; leq ; |a pm b| ; leq ; |a| + |b| $$
其并不是从三角形的三边关系推导而来,考虑 $a,b$ 的正负,将它们做加减,绝对值的和必然都是最大的,绝对值差的绝对值
必然都是最小的。可分类考虑。
