转自：http://blog.sina.com.cn/s/blog_628033fa0100kjjy.html

1.常见误差计算方法：

SSE(和方差、误差平方和)：The sum of squares due to error
MSE(均方差、方差)：Mean squared error
RMSE(均方根、标准差)：Root mean squared error
R-square(确定系数)：Coefficient of determination
Adjusted R-square：Degree-of-freedom adjusted coefficient of determination

一、SSE(和方差)

该统计参数计算的是拟合数据和原始数据对应点的误差的平方和，计算公式如下

二、MSE(均方差)

该统计参数是预测数据和原始数据对应点误差的平方和的均值，也就是SSE/n，和SSE没有太大的区别，计算公式如下

三、RMSE(均方根)

该统计参数，也叫回归系统的拟合标准差，是MSE的平方根，计算公式如下

在这之前，我们所有的误差参数都是基于预测值(y_hat)和原始值(y)之间的误差(即点对点)。

从下面开始是所有的误差都是相对原始数据平均值(y_ba)而展开的(即点对全)!!!

四、R-square(确定系数)

在讲确定系数之前，我们需要介绍另外两个参数SSR和SST，因为确定系数就是由它们两个决定的：

(1)SSR：Sum of squares of the regression，即预测数据与原始数据均值之差的平方和，公式如下

(2)SST：Total sum of squares，即原始数据和均值之差的平方和，公式如下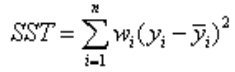

“确定系数”是定义为SSR和SST的比值，故

“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好。

2020-12-26更新————————

2.MAE

https://blog.csdn.net/capecape/article/details/78623897

Mean Absolute Error ，平均绝对误差
是绝对误差的平均值
能更好地反映预测值误差的实际情况.

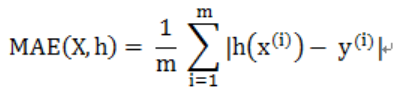
3.RMSE和MAE比较

RMSE也就是第二范数，MAE是第一范数，范数的计算公式：

k越大，即指数越大，对异常值（较大的值）越敏感，RMSE相较于MAE更敏感；

但当异常值少时，符合正态分布，RMSE就表现更好了。

4.MSE到底有没有根号??

https://discuss.pytorch.org/t/how-is-the-mseloss-implemented/12972

torch在实现时非常简单，就是 ((input-target)**2).mean()，平方然后均值这个样子。

https://blog.csdn.net/xiaowei_cqu/article/details/9004193（待看）

天啦，一直都没有，是我记错了。。那个根号应该是针对L2距离（也就是L2范数）的，就是欧几里得距离，而不是MSE

但是这个均值，我还是有问题，为什么不是针对样本，而是针对每个值呢？我明白了，你最后获得这个不也是得需要/len(x)的嘛，也就是针对每个样本的损失了~~~.mean()算是针对每个特征的损失了。