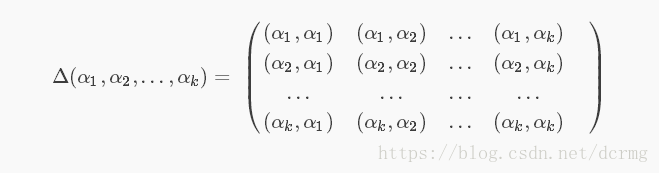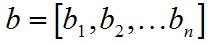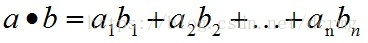Gram定义
n维欧式空间中任意k个向量之间两两的内积所组成的矩阵,称为这k个向量的格拉姆矩阵(Gram matrix)
根据定义可以看到,每个Gram矩阵背后都有一组向量,Gram矩阵就是由这一组向量两两内积得到的,先说一下向量内积是做什么的。
向量的内积,也叫向量的点乘,对两个向量执行内积运算,就是对这两个向量对应位一一相乘之后求和的操作,内积的结果是一个标量。例如对于向量a和向量b:

a和b的内积公式为:
两个向量的内积有什么用呢?一个重要的应用就是可以根据内积判断向量a和向量b之间的夹角和方向关系(详细推导可参见:https://blog.csdn.net/dcrmg/article/details/52416832),具体来说:
a·b>0 方向基本相同,夹角在0°到90°之间
a·b=0 正交,相互垂直
a·b<0 方向基本相反,夹角在90°到180°之间
简单来说就是内积可以反映出两个向量之间的某种关系或联系。Gram矩阵是两两向量的内积组成的,所以Gram矩阵可以反映出该组向量中各个向量之间的某种关系。
风格迁移中的Gram矩阵
深度学习中经典的风格迁移大体流程是:
1. 准备基准图像和风格图像
2. 使用深层网络分别提取基准图像(加白噪声)和风格图像的特征向量(或者说是特征图feature map)
3. 分别计算两个图像的特征向量的Gram矩阵,以两个图像的Gram矩阵的差异最小化为优化目标,不断调整基准图像,使风格不断接近目标风格图像
这里边比较关键的一个是在网络中提取的特征图,一般来说浅层网络提取的是局部的细节纹理特征,深层网络提取的是更抽象的轮廓、大小等信息。这些特征总的结合起来表现出来的感觉就是图像的风格,由这些特征向量计算出来的的Gram矩阵,就可以把图像特征之间隐藏的联系提取出来,也就是各个特征之间的相关性高低。如果两个图像的特征向量的Gram矩阵的差异较小,就可以认定这两个图像风格是相近的。
总的来说,Gram Matrix可看做是图像各特征之间的偏心协方差矩阵(即没有减去均值的协方差矩阵),Gram计算的是两两特征之间的相关性,哪两个特征是同时出现的,哪两个是此消彼长的等等。另一方面,Gram的对角线元素,还体现了每个特征在图像中出现的量,因此,Gram矩阵可以度量各个维度自己的特性以及各个维度之间的关系,所以可以反映整个图像的大体风格。只需要比较Gram矩阵就可以比较两个图像的风格差异了。