
SERIES EXPANSION OF FUNCTIONS, MACLAURIN’S SERIES, TAYLOR’S SERIES, TAYLOR’S FORMULA
Many functions can be represented by polynomials. In this connection let us note a relationship
between the coefficients c0, c1, c2, … ,cn of the polynomial of degree n
1) f(x) = c0 + c1x + c2x2 + … + cnxn
and its derivatives of order one through n at the point x = 0. Let us take the first n derivatives of
polynomial 1):
f ‘(x) = c1 + 2c2x + 3c3x2 + 4c4x3 + …
f ” (x) = 2c2 + 2·3c3x + 3·4c4x2 + …
f ”’ (x) = 2·3c3 + 2·3·4c4x + …
…………………………………………
f(n)(x) = n!cn
Putting x = 0 in the above equations and solving for the c’s we obtain
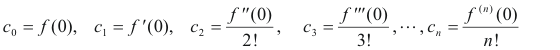
Thus we see that polynomial 1) can be written as
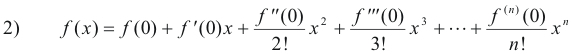
This representation of a polynomial provides us with a means of representing more or less
general functions by polynomials.
There is a completely analogous relationship between the coefficients c0, c1, c2, … ,cn of the
power series in x-a of degree n
3) f(x) = c0 + c1(x-a) + c2(x-a)2 + … + cn(x-a)n
and its derivatives of order one through n at the point x = a. If we take the first n derivatives of
power series 3) we get:
f ‘(x) = c1 + 2c2(x-a) + 3c3(x-a)2 + 4c4(x-a)3 + …
f ” (x) = 2c2 + 2·3c3(x-a) + 3·4c4(x-a)2 + …
f ”’ (x) = 2·3c3 + 2·3·4c4(x-a) + …
…………………………………………
f(n)(x) = n!cn
Putting x = a in the above equations and solving for the c’s we obtain
![]()
Thus we see that power series 3) can be written as
![]()
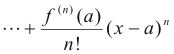
Since a power series is a polynomial, this is another polynomial representation of a function.
Note that 2) is a special case of 4) where a = 0. Also note that if we allow n to increase without
limit 2) and 4) become infinite series. An infinite series of type 2) is called Maclaurin’s series
and an infinite series of type 4) is called Taylor’s series. Such series may be used to represent
rather general functions within some interval of convergence.
When some function f(x) is written in the form of an infinite series, the function is said to be
expanded in an infinite series and the infinite series is said to represent the function in the
interval of convergence.
Maclaurin’s Series. A series of the form
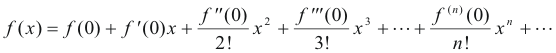
Such a series is also referred to as the expansion (or development) of the function f(x) in powers
of x, or its expansion in the neighborhood of zero. Maclaurin’s series is best suited for finding
the value of f(x) for a value of x in the neighborhood of zero. For values of x close to zero the
successive terms in the expansion grow small rapidly and the value of f(x) can often be
approximated by summing only the first few terms.
A function can be represented by a Maclaurin series only if the function and all its derivatives
exist for x = 0. Examples of functions that cannot be represented by a Maclaurin series: 1/x, ln x,
cot x.
Example 1. Expand ex in a Maclaurin Series and determine the interval of convergence.
Solution. f(x) = ex, f ‘(x) = ex, f ”(x) = ex, f ”'(x) = ex, …….. , f(n)(x) = ex
and
f(0) = 1, f ‘(0) = 1, f ”(0) = 1, f ”'(0) = 1, ……. ,f(n)(0) = 1
so
![]()
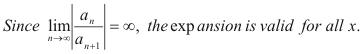
Example 2. Expand sin x in a Maclaurin Series and determine the interval of convergence.
Solution. f(x) = sin x, f'(x) = cos x, f”(x) = – sin x, f”'(x) =- cos x, ……
Since sin 0 = 0 and cos 0 = 1 the expansion is
![]()
It converges for all values of x since
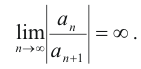
Taylor’s Series. A series of the form
![]()
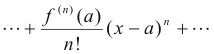
This series is useful for computing the value of some general function f(x) for values of x near a..
The nearer to a the value is, the more quickly the series will converge. When a = 0, Taylor’s
Series reduces, as a special case, to Maclaurin’s Series. If we set x = a + h, another useful form
of Taylor’s Series is obtained:
![]()
In terms analogous to those describing Maclaurin’s expansion, Taylor’s series is called the
development of f(x) in powers of x – a (or h), or its expansion in the neighborhood of a.
Taylor’s Formula with the Remainder. Let a function f(x) and its first n+1
derivatives be continuous on a closed interval containing x = a. Then there is a number x0
between a and x such that
![]()
in which Rn+1(x), the remainder after n + 1 terms, is given by the formula
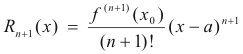
The remainder has been put in several different forms, the usefulness of the form depending on
the particular type of function being expanded. The above form is Lagrange’s form. The
theorem with Lagrange’s form of the remainder is a simple variation of the Extended Law of the
Mean.
Taylor’s theorem is one of the most important theorems in applied analysis. It describes
approximating polynomials for a broad range of functions and provides estimates for errors.
Many of the laws of nature, physical and chemical processes, the motion of bodies, etc. are
expressed with great accuracy by functions which can be expanded in a Taylor’s series.
Theorem 1. The Taylor Series expansion of a function f(x) is a valid representation of the
function for those values of x, and only those values, for which the remainder Rn+1(x) approaches
zero as n becomes infinite.
Maclaurin’s Formula with the Remainder. Let a function f(x) and its first n+1
derivatives be continuous on a closed interval containing x = 0. Then there is a number x0
between 0 and x such that
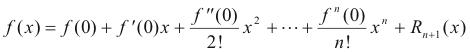
in which Rn+1(x), the remainder after n + 1 terms, is given by the formula
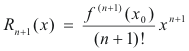
This is a special case of Taylor’s Formula, obtained by letting a = 0.
Theorem 2. The Maclaurin Series expansion of a function f(x) is a valid representation of the
function for those values of x, and only those values, for which the remainder Rn+1(x) approaches
zero as n becomes infinite.
References.
Mathematics, Its Content, Methods and Meaning. Vol I
James and James. Mathematics Dictionary.
Middlemiss. Differential and Integral Calculus.
Oakley. The Calculus. p. 190 – 193
Ayres. Calculus. p. 242, 248
Smith, Salkover, Justice. Calculus. p. 372 – 383
