谈谈异方差性

本文将讨论违背基本假定的另一个方面———异方差性（研究对象为随机扰动项）

第一节 异方差性的概念

一、异方差性的实质

在基本假定中，要求对所有的i(i=1,2,…,n)都有

也就是说ui具有同方差性。这里的方差度量的是随机扰动项围绕其均值的分散程度。由于E(ui)=0，所以可以等价地说，方差度量的是被解释变量Y的观测值围绕回归线的分散程度，同方差性实际指的是相对于回归线被解释变量所有观测值的分散程度相同。

设模型

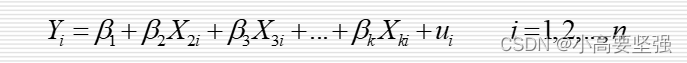
如果其他假定均不变，但模型中随机扰动项ui的方差为：

则称ui具有异方差性。由于异方差性指的是被解释变量观测值的分散程度是随解释变量的变化而变化的，所以可以把异方差看成由某个解释变量的变化而引起的。

二、产生异方差的原因

通常产生异方差有以下主要原因：
（1）模型设定误差
模型的设定主要包括变量的选择和模型数学形式的确定。模型中略去了重要的解释变量常常会导致异方差，省去的解释变量会纳入随机扰动项中，而如果这些影响因素的变化具有差异性，则会对被解释变量产生不同影响，这实际是模型设定问题。
我们知道，可以通过剔除变量的方法去避免多重共线性的影响，但是如果删除了重要的变量又有可能引起异方差性。这是在建模中应当引起注意的问题。除此之外，模型的函数形式不正确，如果把变量间本来为非线性的关系设定为线性，也可能会导致异方差。
（2）测量误差的变化
样本数据的观测误差有可能随着研究范围的扩大而增加，或随着时间得推移逐步积累，也可能随着观测技术的提高而逐步减小。例如，生产函数模型，由于生产要素的投入的增加与生产规模相联系，在其他条件不变的情况下，测量误差可能会随着生产规模的扩大而增加，随机误差项的方差会随着资本和劳动力投入的增加而变化。另外，当用时间序列数据估计生产函数时，随着抽样技术和数据收集处理方法的改进，观测误差有可能会随着时间的推移而降低。
（3）截面数据中总体各单位的差异
通常认为，截面数据较时间序列数据更容易产生异方差。这是因为同一时间不同对象的差异，一般会大于同一对象不同时间的差异。不过，当时间序列数据发生较大变化的情况下，也可能出现比截面数据更严重的异方差。

以上只是对异方差产生的经验总结，在建立模型中，具体产生异方差的原因，还要应对变量的经济意义和数据所表现出的特征进行认真的分析。

第二节 异方差性的后果

一、对参数估计式统计特性的影响

1、参数的OLS估计仍然具有无偏性

由参数估计的统计特性可知，参数OSL估计的无偏性仅依赖于基本假定中误差项的零均值假定（即E(ui)=0），以及解释变量的非随机性，所以，异方差的存在并不影响参数估计式的无偏性。

2、参数OLS估计式的方差不再有效

在模型参数的所有线性估计式中，OLS估计方差最小的重要前提条件之一是随机扰动项为同方差，如果随机扰动项是异方差的，将不能再保证最小二乘估计的方差最小。这时，我们要寻找比OLS估计的方差更小的估计方法。也就是说，在异方差存在时，虽然OLS估计仍保持线性无偏性和一致性，但已失去了有效性，即参数的OLS估计量不再具有最小方差。

二、对模型假设检验的影响

在ui存在异方差时，会严重破坏t检验和F检验的有效性。以一元回归为例，在出现异方差的情况下，参数估计的方差不能用OLS方法去估计，所以通常得到的t统计量与F统计量不再服从t、F分布。因此，一般情况下，只要存在异方差性，在古典假定下用假设检验的统计量可能不在成立。

三、对预测的影响

尽管参数的OLS估计量仍然无偏，并且基于此的预测也是无偏的，但是由于参数估计量不是有效的，对Y的预测也将不是有效的。在ui存在异方差时，方差与xi的变化有关，参数OLS估计的方差Var(Bk估计)不能唯一确定，Y预测区间的建立将产生困难。此外，Var(Bk估计)会增大，Y预测值的精确度也将会下降。

异方差的存在会对回归模型的正确建立和统计推断带来严重的后果，因此在计量经济分析中，有必要检验模型是否存在异方差。

第三节 异方差性的检验

由于随机误差ui不能直接观测，大多数检验异方差的方法都是基于对OLS估计得到的误差ei的分析，只有样本容量比较大时，残差ei才可能是随机误差ui的良好估计，检验方法的运用才有实际意义。

一、图示检验法

1、相关图形分析

方差描述的是随机变量相对其均值的离散程度，而被解释变量Y与随机误差项ui有相同的方差，所以分析Y与X的相关图形，可以粗略地看到Y的离散程度及与X之间是否有相关关系。如果随着X的增加，Y离散程度有逐渐增大（或减小）的变化趋势，则认为存在递增型（或递减型）的异方差。

2、残差图形分析

虽然随机扰动项无法观测，但样本回归的残差一定程度上反映了随机误差的某些分布特征，可以通过残差的图形对异方差性作观察。例如，我们可以使用OLS估计法估计出一元线性回归模型的ei平方，然后绘制ei平方Xi的散点图，如果ei平方不随Xi变化，则表明ui不存在异方差；如果ei平方随着Xi而变化，则表明ui存在异方差。
图示检验法的特点是简单易操作，不足是对异方差性的判断比较粗糙。引起异方差性的原因错综复杂，仅靠图示检验法并不能够准确的确定存在异方差结论，还需要采用其他统计检验方法。

二、Goldfeld-Quandt检验（GQ检验）

GQ检验可用于检验递增性或递减性异方差。此检验的基本思想是将样本分为两部分，然后分别对两个样本进行回归，并计算比较两个回归的剩余平方和是否有明显差异，以此判断是否存在异方差。

1、检验的前提条件

（1）此检验只适用于大样本（n>=30）。
（2）除同方差假定不成立外，其他假定均满足。

2、检验的具体做法

（1）将样本观测值按解释变量Xi的大小排序。
（2）将排列在中间的c个（为样本个数n的1/5~1/4）观察值删除掉，再将剩余的观测值分为两个部分，每部分观察值的个数为(n-c)/2。
（3）提出假设，即H0：两部分数据的方差相等；H1：两部分数据的方差不相等。
（4）构造F统计量。分别对上述两个部分的观察值做回归，由此可以得到两个部分的残差平方和，它们的自由度均为[(n-c)/2]-k，k为参数得个数。若方差为随Xi递增的异方差，在原假设成立的条件下，可导出：

（5）判断。给定显著性水平a，查F分布表，得临界值进行比较。若F*>F(a)，则拒绝原假设，不拒绝备择假设，即认为模型中的随机误差存在异方差。反之，F*<F(a)，则不拒绝原假设，认为模型中随机误差项不存在异方差。

GQ检验的功效，一是与对观测值的正确排序有关；二是与删除数据的个数c有关。经验认为，当n=30时，可以取c=4~6；当n=60时，可以取c=10-14。该方法得到的F分布是近似的，而是只是对异方差是否存在进行判断，在多个解释变量的情况下，对判断是哪一个变量以什么函数形式引起异方差还存在局限。GQ检验也可将样本分为多个组，从中任选两个组进行检验。

三、White检验

White检验的基本思想是，如果存在异方差，其方差与解释变量有关系，分析方差是否与解释变量有某些形式的联系以判断异方差性。但是方差一般是未知的，可用OLS估计的残差平方et平方作为其估计值。在大样本的情况下，作残差平方和与常数项、解释变量、解释变量的平方及其交叉乘积等所构成的辅助回归，利用辅助回归相应的检验统计量，即可判断是否存在异方差性。
为了检验多元线性回归模型的异方差性，以三个解释变量的函数为例。设模型为

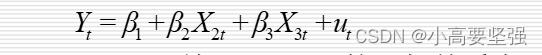
并且，设异方差与X2t、X3t的一般关系为

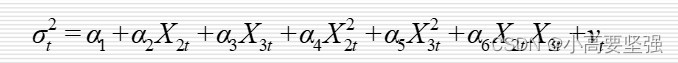
式中，vt为随机误差项。White检验的基本步骤如下：
（1）用OLS法估计公式，计算残差et=Yt-Yt估计，并求出残差的平方et^2。
（2）用残差平方et^2作为异方差的估计，并作其与下列解释变量的辅助回归，即

（3）计算统计量nR^2，其中，n为样本容量，R方为辅助回归的可决系数。
（4）在H0：a2=…=a6=0的条件下，可证明，nR方渐进服从自由度为p的卡方分布，p为辅助回归式中斜率的个数。本例中，辅助回归共有5个解释变量，所以自由度为5。给定显著性水平a，查阅卡方分布表，得出临界值，用nR方与临界值比较，若大于临界值，则拒绝原假设，表明模型中随机误差项存在异方差。

White检验的特点是，不仅能够检验异方差的存在性，同时在多个解释变量的情况下，还能判断出哪一个变量引起的异方差。此方法不需要异方差的先验信息，但要求观测值为大样本。

解释变量过多是White检验的一个缺陷，对于多个解释变量的模型，运用该检验会丧失较多的自由度。为弥补这一不足，有人提出用多元线性回归的拟合值Y估计，作et^2对Y估计与Y估计平方的辅助回归。提出原假设H0:a2=a3=0，运用F检验即可判断模型中的异方差性。这是无论原模型有多少解释变量，要检验的辅助回归模型只有两个约束，因此对自由度影响不大。

四、ARCH检验

时间序列数据中也可能出现异方差性，那么观测时间序列方差变动方法，就是ARCH检验方法。ARCH检验的思想是，在时间序列数据中，可认为存在的异方差性为ARCH过程，并通过检验这一过程是否成立去判断时间序列有无异方差。

1、ARCH过程

设ARCH过程为

式中，p为ARCH过程的阶数，并且a0>0，ai>0(i=1,2,…p)；vt为随机误差。

2、ARCH检验的基本步骤

（1）提出假设。
H0：a1=a2=…=ap=0 H1:aj (j=1,2,…p)中至少有一个不为零。
（2）对原模型作OLS估计，求出残差et，并计算残差平方序列et方,et-1方…，以分别作为随机扰动项及其滞后项的估计。
（3）做辅助回归。

式中et方估计表示et方的估计。
（4）计算辅助回归的可决系数R方，可以证明，在原假设H0成立条件下，基于大样本，有(n-p)R方渐进服从自由度为p的卡方分布，p就是误差项滞后期数。给定显著性水平a，查卡方分布表得出临界值，如果(n-p)R方大于临界值，则拒绝原假设，表明模型中的随机扰动项存在异方差。

ARCH检验的特点是，要求变量的观测值为大样本，并且是时间序列数据，它只能判断模型中是否存在异方差，而不能诊断出是哪一个变量引起的异方差。

五、Glejser检验

Glejser检验的基本思想是，由OLS法得到残差ei，取ei的绝对值，然后并对某个解释变量Xi回归，根据回归模型的显著性和拟合优度来判断是否存在异方差。该检验的特点是不仅能对异方差的存在进行判断，而且能对异方差随某个解释变量变化的函数形式进行诊断。该检验要求变量的观测值为大样本。

Glejser检验的具体步骤如下：
（1）利用样本数据构建回归模型求得残差序列ei=Yi-Yi的估计
（2）用残差绝对值对Xi进行回归，由于ei的绝对值与Xi的真实函数形式并不知道，可用各种函数形式去实验，从中选择最佳形式。
（3）根据选择的函数形式作ei绝对值对Xi的回归，用回归所得到的R方、t、F等信息判断，若参数B显著不为零，则认为存在异方差性。

这些检验方法的共同思想是，基于不同的假定，分析随机误差项的方差与解释变量之间的相关性，以判断随机误差项的方差是否随着解释变量而变化。其中有的检验方法还能提供随机误差项的方差与解释变量而变化。其中有的检验方法还能提供随机误差项的方差与解释变量之间的某些信息，这些信息对补救异方差性可能是有价值的。

第四节 异方差性的补救措施

通过检验发现确实存在异方差，则需要采取措施对异方差进行修正，基本思想是在确认异方差形式的基础上，采用适当的估计方法，消除或减小异方差对模型的影响。

一、对模型变换

当可以确定异方差具体形式时，可以对模型进行适当变换，可能会消除或减轻异方差的影响。以一元线性回归模型为例：

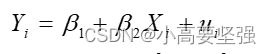
经检验ui存在异方差，并已知ui的方差是解释变量的函数，即：

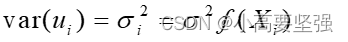
其中f(Xi)>0。显然当f(Xi)为常数时，ui为同方差，当f(Xi)不是常数时，ui为异方差。为了变换模型，左右两边除以根号f(Xi)，得

可见，经变换后的随机误差项已经是同方差。
根据图示检验法或Glejser检验所得到的相应信息，可以对f(xi)的函数形式做出各种假定，常见的f(Xi)形式及vi的对应情况有如下几种：

在异方差的形式已知或通过检验能够确定的前提下，运用上述模型变换的方法可以较好地修正异方差对模型的影响。但在大多数情况下，异方差形式并不知道，可以选用其他方法来确定。

另外，异方差性现象可视为模型设定偏误的一种特殊形式。因此，修正异方差的一种有效方法是重新设定回归模型形式，以消除异方差。

二、加权最小二乘法

还是以一元线性回归模型为例。按照最小二乘法的基本原则，是使残差平方和最小。在同方差性假定下，普通最小二乘法是把每个残差平方都同等看待，都赋予相同的权数1.但是当存在异方差性时，方差oi方越小，其样本值偏离均值的程度越小，其观测值越应受到重视，即方差越小，在确定回归线时的作用应当越大；反之，如果方差oi方越大，其样本值偏离均值的程度越大，其观测值所起到的作用应当越小。

也就是说，在拟合存在异方差的模型的回归线时，对不同的oi方应该区别对待。从样本的角度，对较小的ei方给予较大的权数，对较大的ei方给予较小的权数，从而使残差平方和更好地反映oi方对残差平方和的影响。通常可将权数取为wi=1/(oi^2)（i=1,2…,n），由此oi方越小时，wi越大，当oi方越大时，wi就越小。将权数与残差平方相乘以后再求和，得

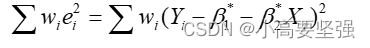
根据最小二乘原理，若使得加权的残差平方和最小，即

这样估计出的参数B1估计和B2估计称为加权最小二乘估计。这种求解参数估计式的方法为加权最小二乘（weighted least square，WLS）法。

这里扩展指出，用模型变换法，然后用OLS估计其参数，实际与应用加权最小二乘估计的参数是一致的。这也间接证明了加权最小二乘法可以消除异方差。

三、模型的对数变换

在经济意义成立的情况下，对一元线性回归模型作对数变换，其变量Yi和Xi分别用LnYi和LnXi代替，即

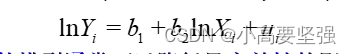
对数变换后的模型通常可以降低异方差性的影响。

首先，运用对数变换能使测定变量值的尺度缩小。它可以将两个数值之间原来10倍的差异缩小到只有2倍的差异，例如100是10的10倍，而lg100=2是lg10的两倍。
其次，经过对数变换后的线性模型，其残差e表示相对误差，而相对误差往往对绝对误差有较小的差异。
但是特别要注意的是，对变量取对数虽然能降低异方差对模型的影响，但应注意取对数后变量的经济意义。如果变量之间在经济意义上并非呈对数线性关系，则不能简单地对变量取对数，这是只能用其他方法对异方差进行修正。

通常一般可以分析经济中弹性相关问题。

本文主要参考庞皓计量经济学第三版