复习使用
定义
图灵机形式定义:
TMm=(Q,Σ,Γ,δ,q0,qaccept,qreject)TM m=(Q,\Sigma,\Gamma,\delta,q_{0},q_{accept},q_{reject})TMm=(Q,Σ,Γ,δ,q0,qaccept,qreject)
(1)QQQ是状态集
(2)Σ\SigmaΣ编入定义表
(3)Γ\GammaΓ带定义表,ε⊆Γ,⊔⊆Γ\varepsilon \subseteq \Gamma,\sqcup \subseteq\Gammaε⊆Γ,⊔⊆Γ
(4)δ:Q×Γ→Q×Γ×{L,R}\delta:Q\times\Gamma\to Q \times \Gamma \times\{L,R\}δ:Q×Γ→Q×Γ×{L,R}
(5)q0q_0q0为初态
(6)qacceptq_{accept}qaccept为接受状态
(7)qrejectq_{reject}qreject为拒绝状态
格局
我们用格局表示图灵机的当前状态,当前带内容和读写头的当前位置的信息。

上图就是一种格局,我们表示为1011q7011111011q_7011111011q701111,意思为:当前带内容是101101111,当前状态为q7q_7q7,读写头当前在第二个0上。格局中状态后的第一个字符为读写头指向的位置。
如果图灵机能合法的从格局C1C_1C1一步进入到C2C_2C2,则称格局C1C_1C1产生格局C2C_2C2,可表示为C1→MC2C_1 \underset{M}{\rightarrow} C_2C1M→C2,这个概念的形式定义如下:
设a,b和c是Γ\GammaΓ中的符号,u和v是Γ∗\Gamma^{*}Γ∗中的字符串,qiq_iqi和qjq_jqj是状态,则uaqibvuaq_ibvuaqibv和uqjacvuq_jacvuqjacv是两个格局。如果转移函数满足δ(qi,b)=(qj,c,L)\delta(q_i,b)=(q_j,c,L)δ(qi,b)=(qj,c,L),则说:
uaqibvuaq_ibvuaqibv产生uqjacvuq_jacvuqjacv
这说明了图灵机左移的情况,下面是右移的情况。如果δ(qi,b)=(qj,c,R)\delta(q_i,b)=(q_j,c,R)δ(qi,b)=(qj,c,R),则说:
uaqibvuaq_ibvuaqibv产生uacqjvuacq_jvuacqjv
图灵机与DFA的区别
DFA:确定性有穷自动机
1.带上可读写
2.读写头可左右移动
3.带子无限长
4.接受和拒绝状态都会停机
其他相关定义
如果L(M)={w∈Σ∗∣∃u,v∈Γ∗,q0w→M∗uqacceptv}L(M)=\{w\in \Sigma^* |\exists u,v \in \Gamma^*,q_{0}w\xrightarrow[M]{*}uq_{accept}v\}L(M)={w∈Σ∗∣∃u,v∈Γ∗,q0w∗Muqacceptv}称www是M接受(识别)的语言。
图灵可识别的/递归可枚举的(r.e.r.e.r.e.),定义为:
L⊆Σ∗,r.e.⇔∃TMM(L=L(M))⇔∃TMM(∀w∈L,∃u,v∈Γ∗,(q0w∣→M∗uqacceptv))L\subseteq \Sigma^*,r.e.\Leftrightarrow \exists TM M(L=L(M))\Leftrightarrow\exists TM M\left ( \forall w \in L,\exists u,v \in \Gamma^*, \left ( q_0w |\xrightarrow[M]{*}uq_{accept}v\right )\right )L⊆Σ∗,r.e.⇔∃TMM(L=L(M))⇔∃TMM(∀w∈L,∃u,v∈Γ∗,(q0w∣∗Muqacceptv))
图灵可判定的/图灵可递归的(recusive),定义为:
L⊆Σ∗⇔∃TMM(∀w∈L,∃u,v∈Γ∗,(q0w∣→M∗uqacceptv)∧∀wˉ∉L,∃uˉ,vˉ∈Γ∗,(q0wˉ∣→M∗uˉqrejectvˉ))L\subseteq\Sigma^* \Leftrightarrow \exists TM M\left ( \forall w \in L,\exists u,v \in \Gamma^*, \left ( q_0w| \xrightarrow[M]{*}uq_{accept}v\right )\wedge\forall \bar{w} \notin L,\exists\bar{u},\bar{v} \in \Gamma^*, \left ( q_0\bar{w}| \xrightarrow[M]{*}\bar{u}q_{reject}\bar{v}\right ) \right )L⊆Σ∗⇔∃TMM(∀w∈L,∃u,v∈Γ∗,(q0w∣∗Muqacceptv)∧∀wˉ∈/L,∃uˉ,vˉ∈Γ∗,(q0wˉ∣∗Muˉqrejectvˉ))
可递归的与可枚举的区别
1)可枚举的
在输入上运行TM时,可能达到停机状态,也可能达到循环即不停机状态
如果在,可达到这个状态,如果不在,没有回答
2)可判定的
对于任何输入,TM总能决定接受或者拒绝
如果在,可达到接受状态,如果不在,达到拒绝状态
可递归的与可枚举的联系
1)可判定的都是可识别的,可识别的不一定都是可判定的
2)设L⊆Σ∗,Lˉ=Σ∗−L,L is recusive,  ⟺  L和Lˉ都是r.e.L\subseteq\Sigma^*,\bar{L}=\Sigma^*-L,L \, is \,recusive,\iff L和\bar{L}都是r.e.L⊆Σ∗,Lˉ=Σ∗−L,Lisrecusive,⟺L和Lˉ都是r.e.
不是可识别的
ATM‾、EQTM、EQTM‾、ETM\overline{A_{TM}}、EQ_{TM}、\overline{EQ_{TM}}、E_{TM}ATM、EQTM、EQTM、ETM
不是可递归的
ATM、ATM‾、ETM、NETM、HALTTM、PCP、REGULARTMA_{TM}、\overline{A_{TM}}、E_{TM}、NE_{TM}、HALT_{TM}、PCP、REGULAR_{TM}ATM、ATM、ETM、NETM、HALTTM、PCP、REGULARTM
通用图灵机:
ATM={<M,w>∣TM M接受w}A_{TM}=\{<M,w>|TM \, M接受w\}ATM={<M,w>∣TMM接受w},ATM is  r.e.(图灵可识别的),ATM是不可判定的A_{TM} \,is\,\,r.e.(图灵可识别的),A_{TM}是不可判定的ATMisr.e.(图灵可识别的),ATM是不可判定的
构造TM U识别ATMTM \,U识别A_{TM}TMU识别ATM
U="U="U="对输入<M,w>,其中M是一个TM,w是一个串<M,w>,其中M是一个TM,w是一个串<M,w>,其中M是一个TM,w是一个串:
\quad\quad\quad\quad\quad\quad\quad\quad在输入w上模拟MMM
\quad\quad\quad\quad\quad\quad\quad\quad若MMM停机,则停机"""
注意:如果MMM在www上循环,则UUU在输入<M,w><M,w><M,w>上循环,这就是UUU不能判定ATMA_{TM}ATM的原因。假如MMM知道自己在www上不停机,他能拒绝www,但事实上,它不知道。图灵机UUU是通用图灵机的一个例子。通用图灵机能模拟任何其他图灵机。
TM UTM \,UTMU识别MMM
语言间的关系:

归约:
A,B两个问题(语言),A归约到B,若B可解,则A可解;若A不可解,则B不可解
时间复杂性
最坏情况分析:考虑在某特定长度的所有输入上的运行时间的最大值
平均情况分析:考虑在某特定长度的所有输入上运行时间的平均值
定义:令MMM是一个在所有输入上都停机的确定型图灵机,MMM的运行时间(时间复杂度)是一个函数f:N→Nf:N\rightarrow Nf:N→N,其中f(n)f(n)f(n)是MMM在所有长度n的输入上运行所经过的最大步数。若f(n)f(n)f(n)是M的运行时间,则称M在时间f(n)f(n)f(n)内运行,MMM是f(n)f(n)f(n)的时间图灵机。
大O记法:
f,g:N→R+,称f(n)=O(g(n))f,g:N\rightarrow R^+,称f(n)=O(g(n))f,g:N→R+,称f(n)=O(g(n))
若∃c∈N+,∃n0∈N+,∀(n>=n0→f(n)<=cg(n))若\exist c \in N^+ ,\exist n_0 \in N^+ ,\forall( n >=n_0 \rightarrow f(n)<=cg(n))若∃c∈N+,∃n0∈N+,∀(n>=n0→f(n)<=cg(n))
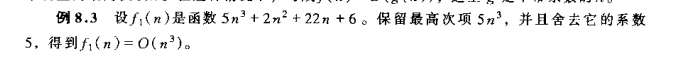
小o记法:
f,g:N→R+,称f(n)=O(g(n))f,g:N\rightarrow R^+,称f(n)=O(g(n))f,g:N→R+,称f(n)=O(g(n))
若limn→∞f(n)g(n))=0,∀c>0,∃n0∈N+,∀(n>=n0→f(n)<cg(n))若\lim_{n\to \infty }\frac{f(n)}{g(n))}=0,\forall c >0 ,\exist n_0 \in N^+ ,\forall( n >=n_0 \rightarrow f(n)<cg(n))若limn→∞g(n))f(n)=0,∀c>0,∃n0∈N+,∀(n>=n0→f(n)<cg(n))


时间复杂性类(time complexity class)
TIME(t(n))
令t:N→N,TIME(t(n))=L∣L是O(t(n))时间TM可判定的t:N\rightarrow N,TIME (t(n))={L|L是O(t(n))时间TM可判定的}t:N→N,TIME(t(n))=L∣L是O(t(n))时间TM可判定的
TMN是一个非确定的判定其,f:N→NTM N是一个非确定的判定其,f:N\rightarrow NTMN是一个非确定的判定其,f:N→N
N的时间复杂性f(n)是任意长度为n的输入上,N的所有分支达到接受态/最大的步数N的时间复杂性f(n)是任意长度为n的输入上,N的所有分支达到接受态/最大的步数N的时间复杂性f(n)是任意长度为n的输入上,N的所有分支达到接受态/最大的步数
定义NTIME(t(n))=L∣L是O(t(n))时间NTM可判定的定义 NTIME(t(n))={L|L是O(t(n))时间NTM可判定的}定义NTIME(t(n))=L∣L是O(t(n))时间NTM可判定的
P类问题: TM多项式时间可判定的问题
NP类问题:NTM多项式时间可判定的问题
定理
1.设L⊆Σ∗,Lˉ=Σ∗−L,L is recusive,  ⟺  L和Lˉ都是r.e.L\subseteq\Sigma^*,\bar{L}=\Sigma^*-L,L \, is \,recusive,\iff L和\bar{L}都是r.e.L⊆Σ∗,Lˉ=Σ∗−L,Lisrecusive,⟺L和Lˉ都是r.e.
证明:1.必要性
1)显然L是可递归的⇒\Rightarrow⇒L是递归可枚举的
2)L是可递归的⇒Lˉ\Rightarrow\bar{L}⇒Lˉ是可递归的⇒Lˉ\Rightarrow\bar{L}⇒Lˉ是递归可枚举的
2.充分性
1)设L(M)=L,L(Mˉ)=LˉL(M)=L,L(\bar{M})=\bar{L}L(M)=L,L(Mˉ)=Lˉ,构造TMOTM OTMO如下:两个带上并行模拟M和Mˉ\bar{M}Mˉ,M接受,则O接受;Mˉ\bar{M}Mˉ接受,则O拒绝,而w∈L(M)w\in L(M)w∈L(M)或w∈L(Mˉ)w\in L(\bar{M})w∈L(Mˉ),故O必判定w,因此O判定L,L是递归的
存在性
使用反证法+对角线法证明
3.令x={0,1},则xw是不可数的,xw是0,1无限序列的集合x=\left \{ 0,1 \right \},则 x^w是不可数的,x^w是0,1无限序列的集合x={0,1},则xw是不可数的,xw是0,1无限序列的集合
证明:设g:z+→xwg:z^+\rightarrow x^wg:z+→xw,得证ggg不是满射(surjectivemap)
假设ggg是一个满射,记g(i)=xi1…xii…xijg\left(i\right)=x_{i1}…x_{ii}…x_{ij}g(i)=xi1...xii...xij
其中,xi,j∈{0,1},i,j∈z+x_{i,j}\in \left \{ 0,1 \right \},i,j \in z^+xi,j∈{0,1},i,j∈z+,构造y=y1y2….yk….y=y_1y_2….y_k….y=y1y2....yk....
使得yk=1−xkk,k∈z+y_k=1-x_{kk},k\in z^+yk=1−xkk,k∈z+
显然,y∈xwy\in x^wy∈xw
由于y的第k位于g(x)的第k位不同,k∈z+k \in z^+k∈z+
故有y∉{g(k)∣k∈z+}y \notin \{ g(k)|k \in z^+\}y∈/{g(k)∣k∈z+}
即y不在g的象中
矛盾
因而g不是满射,故xwx^wxw是不可数的
4.设A是一个集合,则A与zAz^AzA不是一一对应的,zA=P(A)z^A=\mathbb{P}(A)zA=P(A)
注:zAz^AzA是A的所有子集所组成的集合
证明:只须证明g:A→P(A)g:A\rightarrow\mathbb{P}(A)g:A→P(A)不是满射即可
反证:假设g是一个满射
令B={a∈A∣a∉g(a)}B=\{a\in A|a\notin g(a)\}B={a∈A∣a∈/g(a)}
由于B⊆AB\subseteq AB⊆A,则存在b∈A,满足g(b)=Bb\in A,满足g(b)=Bb∈A,满足g(b)=B
则有b∈B⇔b∉Bb\in B \Leftrightarrow b\notin Bb∈B⇔b∈/B
矛盾,故g不是满射,A与zAz^AzA不是一一对应的
解释:
存在b∈A,满足g(b)=Bb\in A,满足g(b)=Bb∈A,满足g(b)=B(因为满射,所以对于B一定有b∈Ab\in Ab∈A与之对应)
则有b∈B⇔b∉Bb\in B \Leftrightarrow b\notin Bb∈B⇔b∈/B
(若b∈B⇒b∉g(b)⇒b∉Bb\in B\Rightarrow b\notin g(b)\Rightarrow b\notin Bb∈B⇒b∈/g(b)⇒b∈/B,若b∉B且b∈A⇒b∈A并且b∈g(b)⇒b∈Bb\notin B且b\in A \Rightarrow b\in A 并且 b\in g(b)\Rightarrow b\in Bb∈/B且b∈A⇒b∈A并且b∈g(b)⇒b∈B)
5.设ATM={<M,w>∣TM M接受w}A_{TM}=\{<M,w>|TM \, M接受w\}ATM={<M,w>∣TMM接受w},则ATMA_{TM}ATM不是递归的,不是图灵可判定的。
证明:设ATMA_{TM}ATM是可判定的,则判定器为HHH。
H(<M,w>)={accept,if M acceptreject,if M rejectH(<M,w>)=\left\{\begin{matrix} accept,if \, M \, accept\\ reject,if \, M \, reject \end{matrix}\right.H(<M,w>)={accept,ifMacceptreject,ifMreject
构造TM DTM\, DTMD,使HHH成为其子程序,识别HHH的行为,DDD则与其行为相反,则
D(<M>)={accept,if M reject <M>reject,if M accept <M>D(<M>)=\left\{\begin{matrix} accept,if \, M \, reject \,<M>\\ reject,if \, M \, accept\, <M> \end{matrix}\right.D(<M>)={accept,ifMreject<M>reject,ifMaccept<M>
若输入<D><D><D>,则有
D(<D>)={accept,if D reject d<D>reject,if D accept <D>D(<D>)=\left\{\begin{matrix} accept,if \, D \, reject \,d <D>\\ reject,if \, D \, accept \, <D> \end{matrix}\right.D(<D>)={accept,ifDrejectd<D>reject,ifDaccept<D>
有D接受<D>⇔D拒绝<D>有D接受<D> \Leftrightarrow D拒绝<D>有D接受<D>⇔D拒绝<D>,矛盾,
因而 ,ATMA_{TM}ATM不是可判定的
注:这个问题被称为接受问题
6.ATM={<M,w>∣TM M接受w}A_{TM}=\{<M,w>|TM \, M接受w\}ATM={<M,w>∣TMM接受w},ATM is  r.e.(图灵可识别的)A_{TM} \,is\,\,r.e.(图灵可识别的)ATMisr.e.(图灵可识别的)
证明:构造TM U="TM \,U="TMU="对输入<M,w><M,w><M,w>:
\quad\quad\quad\quad\quad\quad\quad\quad在串上模拟MMM对输入www的动作,
\quad\quad\quad\quad\quad\quad\quad\quad若MMM停机,则停机"""
TM UTM \,UTMU识别MMM
7.ATM‾\overline{A_{TM}}ATM不是图灵可识别的,即不是递归可枚举的
证明:因为ATMA_{TM}ATM是递归可枚举的,若ATM‾\overline{A_{TM}}ATM也是递归可枚举的,根据定理可得,ATMA_{TM}ATM是可判定的,与ATMA_{TM}ATM是不可判定的,矛盾,ATM‾\overline{A_{TM}}ATM不是图灵可识别的。
归约性
停机问题:
8.HALTTM={<M,w>∣TM M∧M对w停机}HALT_{TM}=\{<M,w>|TM\,M \wedge M对w停机 \}HALTTM={<M,w>∣TMM∧M对w停机}
HALTTMHALT_{TM}HALTTM是不可判定的,即不是递归的
证明方法:1).可以使用对角线法证明
2).使用归约法证明
ATM归约到HALTTMA_{TM}归约到HALT_{TM}ATM归约到HALTTM
证明(归约法):
假设TM R判定HALTTM,基于TM R构造TM S,使得TM S判定ATMTM\, R判定HALT_{TM},基于TM\,R构造TM\,S,使得TM\,S判定A_{TM}TMR判定HALTTM,基于TMR构造TMS,使得TMS判定ATM
S="输入<m,w>:S="输入<m,w>:S="输入<m,w>:
\quad\quad在输入<m,w><m,w><m,w>上运行TM RTM\,RTMR,
\quad\quad(1)若RRR拒绝,<m,w>∉ATM<m,w>\notin A_{TM}<m,w>∈/ATM,SSS拒绝
\quad\quad(2)若RRR接受,<m,w>∈HALTTM<m,w>\in HALT_{TM}<m,w>∈HALTTM,MMM对www停机:
\quad\quad\quad MMM接受www,SSS接受
\quad\quad\quad MMM拒绝www,SSS拒绝
若R判定HALTTM,则S判定ATMR判定HALT_{TM},则S判定A_{TM}R判定HALTTM,则S判定ATM,但ATMA_{TM}ATM不是递归的,所以HALTTMHALT_{TM}HALTTM不是递归的
ETM={<M>∣TM M∧L(M)=ϕ}E_{TM}=\{<M>|TM\,M \wedge L(M)=\phi \}ETM={<M>∣TMM∧L(M)=ϕ}
NETM={<M>∣TM M∧L(M)不等于ϕ}NE_{TM}=\{<M>|TM\,M \wedge L(M) 不等于 \phi \}NETM={<M>∣TMM∧L(M)不等于ϕ}
9.ETM,NETME_{TM},NE_{TM}ETM,NETM不是递归的
证明:
(1)NETM是r.e.的NE_{TM}是r.e.的NETM是r.e.的
利用通用TM UTM\,UTMU构造TM TTM\,TTMT
T="对于TM M的编码<M>TM\,M的编码<M>TMM的编码<M>
(1)猜测一系列M的输入wi∈Σ∗w_i\in\Sigma^*wi∈Σ∗
(2)在输入<M,w><M,w><M,w>上运行TM UTM\,UTMU
若M接受wiw_iwi,则接受
这样,若L(M)不等于ϕL(M) 不等于\phiL(M)不等于ϕ,则<M>∈L(T)<M>\in L(T)<M>∈L(T)
反之,若L(M)=ϕL(M) =\phiL(M)=ϕ,则<M>∉L(T)<M>\notin L(T)<M>∈/L(T)
故L(T)=NETM,NETM是r.e.的L(T)=NE_{TM},NE_{TM} 是r.e.的L(T)=NETM,NETM是r.e.的
(2)NETM不是递归的NE_{TM}不是递归的NETM不是递归的
ATM归约到NETMA_{TM}归约到NE_{TM}ATM归约到NETM
假设TM N判定NETM,基于TM N构造TM A,使得TM A判定ATMTM\, N判定NE_{TM},基于TM\,N构造TM\,A,使得TM\,A判定A_{TM}TMN判定NETM,基于TMN构造TMA,使得TMA判定ATM
S="对输入<m,w>:S="对输入<m,w>:S="对输入<m,w>:
\quad\quad 1)构造TM UTM\,UTMU="对输入x:模拟M运行w,若M接受w,则U接受xx:模拟M运行w,若M接受w,则U接受xx:模拟M运行w,若M接受w,则U接受x,
\quad\quad 2)在输入<U>上运行N在输入<U>上运行N在输入<U>上运行N
\quad\quad\quad NNN接受UUU,AAA接受
\quad\quad\quad NNN拒绝UUU,AAA拒绝
显然,若TM N判定N,则TM A判定ATMTM\,N判定N,则TM\,A判定A_{TM}TMN判定N,则TMA判定ATM,而ATMA_{TM}ATM不是递归的,所以NETMNE_{TM}NETM不是递归的
(3)由(1)(2)可知,ETM不是r.e.的E_{TM}不是r.e.的ETM不是r.e.的,故ETM不是递归的E_{TM}不是递归的ETM不是递归的。
或:
NETM不是递归的NE_{TM}不是递归的NETM不是递归的,
若ETM是递归的E_{TM}是递归的ETM是递归的,NETM=ETM‾NE_{TM}=\overline{E_{TM}}NETM=ETM,NETM是递归的NE_{TM}是递归的NETM是递归的,所以ETM不是递归的E_{TM}不是递归的ETM不是递归的
10.Res定理
r.e.r.e.r.e.语言的非平凡性质是不可判定的
注:问题L⊆Σ∗L\subseteq \Sigma^{*}L⊆Σ∗
\quad 性质P⊆ZΣ∗\mathbb{P}\subseteq Z^{ \Sigma^{*}}P⊆ZΣ∗
非平凡的P不等于ϕ,P不等于ZΣ∗\mathbb{P}不等于\phi,\mathbb{P}不等于Z^{ \Sigma^{*}}P不等于ϕ,P不等于ZΣ∗
注:P\mathbb{P}P既不为空,也不为所有语言的集合
推论:
REGULARTM={<M>∣TMM∧L(M)是正则的}\quad REGULAR_{TM}=\{<M>|TM_{M}\wedge L(M)是正则的\}REGULARTM={<M>∣TMM∧L(M)是正则的}
EQTM={<M1M2>∣TMM1,M2∧L(M1)=L(M2)}\quad EQ_{TM}=\{<M_1M_2>|TM M_1,M_2\wedge L(M_1)=L(M_2)\}EQTM={<M1M2>∣TMM1,M2∧L(M1)=L(M2)}
11.POST问题(不重要)
定义:计算历史
TM M,M∈Σ∗,M在w上的计算历史是一个格局系列:C1,C2,…,CiTM\,M,M\in \Sigma^*,M在w上的计算历史是一个格局系列:C_1,C_2,…,C_iTMM,M∈Σ∗,M在w上的计算历史是一个格局系列:C1,C2,...,Ci
其中C1是M在w上的起始格局,且Ci∣—Cm,i=1,2,….其中C_1是M在w上的起始格局,且C_i|—C_m,i=1,2,….其中C1是M在w上的起始格局,且Ci∣—Cm,i=1,2,....
若Cl为接受格局,则称为接受历史若C_l为接受格局,则称为接受历史若Cl为接受格局,则称为接受历史
若Cl为拒绝格局,则称为拒绝历史若C_l为拒绝格局,则称为拒绝历史若Cl为拒绝格局,则称为拒绝历史
POST对应问题


计算层次:
| 语言类别 | 计算过程 | 计算层次 | 注 |
|---|---|---|---|
| 递归的 | 算法 | 可计算的 | 可数的 |
| 递归可枚举的 | 程序 | 半可计算的 | 可数的 |
| 非r.e.的 | 无 | 不可计算的 | 不可数的 |
映射可归约性

12.EQTM既不是r.e.的,也不是补r.e.的(即EQTM‾不是r.e的)}EQ_{TM}既不是r.e.的,也不是补r.e.的(即\overline{EQ_{TM}}不是r.e的)\}EQTM既不是r.e.的,也不是补r.e.的(即EQTM不是r.e的)}
分析:要证EQTM不是r.e.的,即证ATM‾≤mEQTM,根据定理可得,只需证明ATM≤mEQTM‾EQ_{TM}不是r.e.的,即证\overline{A_{TM}}\leq mEQ_{TM},根据定理可得,只需证明A_{TM}\leq m\overline{EQ_{TM}}EQTM不是r.e.的,即证ATM≤mEQTM,根据定理可得,只需证明ATM≤mEQTM
证明:
<1>EQTM不是r.e.的EQ_{TM}不是r.e.的EQTM不是r.e.的
计算f的图灵机为:计算f的图灵机为:计算f的图灵机为:
F=“对输入<M,w>:\quad F=“对输入<M,w>:F=“对输入<M,w>:
1.构造M1,M2\quad\quad 1.构造M_1,M_21.构造M1,M2
M1=“对x拒绝”\quad\quad M_1=“对x拒绝”M1=“对x拒绝”
M2=“对x,模拟M执行w,若M接受,则M2接受”\quad\quad M_2=“对x,模拟M执行w,若M接受,则M_2接受”M2=“对x,模拟M执行w,若M接受,则M2接受”
2.输出<M1,M2>\quad\quad 2.输出<M_1,M_2>2.输出<M1,M2>
由F:ATM≤mEQTM‾由F:A_{TM}\leq m\overline{EQ_{TM}}由F:ATM≤mEQTM
F是可计算函数F是可计算函数F是可计算函数
<M,w>∈ATM⇔<M1,M2>∈EQTM‾<M,w>\in A_{TM}\Leftrightarrow <M_1,M_2>\in \overline{EQ_{TM}}<M,w>∈ATM⇔<M1,M2>∈EQTM
故ATM‾≤mEQTM故\overline{A_{TM}}\leq mEQ_{TM}故ATM≤mEQTM
而ATM‾不是r.e.的,故EQTM不是r.e.的而\overline{A_{TM}}不是r.e.的, 故EQ_{TM}不是r.e.的而ATM不是r.e.的,故EQTM不是r.e.的
<2>EQTM‾不是r.e.的\overline{EQ_{TM}}不是r.e.的EQTM不是r.e.的
计算g的图灵机为:计算g的图灵机为:计算g的图灵机为:
G=“对输入<M,w>:\quad G=“对输入<M,w>:G=“对输入<M,w>:
1.构造M1,M2\quad\quad 1.构造M_1,M_21.构造M1,M2
M1=“对x接受”\quad\quad M_1=“对x接受”M1=“对x接受”
M2=“对x,模拟M执行w,若M接受,则M2接受”\quad\quad M_2=“对x,模拟M执行w,若M接受,则M_2接受”M2=“对x,模拟M执行w,若M接受,则M2接受”
2.输出<M1,M2>\quad\quad 2.输出<M_1,M_2>2.输出<M1,M2>
由G:ATM≤mEQTM由G:A_{TM}\leq mEQ_{TM}由G:ATM≤mEQTM
G是可计算函数G是可计算函数G是可计算函数
<M,w>∈ATM⇔<M1,M2>∈EQTM<M,w>\in A_{TM}\Leftrightarrow <M_1,M_2>\in EQ_{TM}<M,w>∈ATM⇔<M1,M2>∈EQTM
故ATM‾≤mEQTM‾故\overline{A_{TM}}\leq m\overline{EQ_{TM}}故ATM≤mEQTM
而ATM‾不是r.e.的,故EQTM‾不是r.e.的而\overline{A_{TM}}不是r.e.的, 故\overline{EQ_{TM}}不是r.e.的而ATM不是r.e.的,故EQTM不是r.e.的
13.计算x+yx+yx+y
x的编码,记为<x>=1x<x>=1^x<x>=1x
y的编码,记为<y>=1y<y>=1^y<y>=1y
TMm=(Q,Σ,Γ,δ,q0,qaccept,qreject)TM m=(Q,\Sigma,\Gamma,\delta,q_{0},q_{accept},q_{reject})TMm=(Q,Σ,Γ,δ,q0,qaccept,qreject)
(1)Q={q0,q1,q2,q3,qaccept,qreject}Q=\{q_0,q_1,q_2,q_3,q_{accept},q_{reject}\}Q={q0,q1,q2,q3,qaccept,qreject}
(2)Σ={0,1}\Sigma=\{0,1\}Σ={0,1}
(3)Γ={0,1,⊔}\Gamma=\{0,1,\sqcup \}Γ={0,1,⊔}
(4)δ\deltaδ的定义
| – | 0 | 1 | ⊔\sqcup⊔ |
|---|---|---|---|
| q0q_0q0 | (qreject,0,R)(q_{reject},0,R)(qreject,0,R) | (q1,1,R)(q_{1},1,R)(q1,1,R) | (qreject,⊔,R)(q_{reject},\sqcup,R)(qreject,⊔,R) |
| q1q_1q1 | (qreject,0,R)(q_{reject},0,R)(qreject,0,R) | (q1,1,R)(q_{1},1,R)(q1,1,R) | (q2,1,R)(q_{2},1,R)(q2,1,R) |
| q2q_2q2 | (qreject,0,R)(q_{reject},0,R)(qreject,0,R) | (q2,1,R)(q_{2},1,R)(q2,1,R) | (q3,⊔,L)(q_{3},\sqcup,L)(q3,⊔,L) |
| q3q_3q3 | (qreject,0,R)(q_{reject},0,R)(qreject,0,R) | (qaccept,⊔,R)(q_{accept},\sqcup,R)(qaccept,⊔,R) | (qreject,⊔,R)(q_{reject},\sqcup,R)(qreject,⊔,R) |
| qacceptq_{accept}qaccept | HALT | HALT | HALT |
| qrejectq_{reject}qreject | HALT | HALT | HALT |
(5)q0q_0q0为初态
(6)qacceptq_{accept}qaccept为接受状态
(7)qrejectq_{reject}qreject为拒绝状态
解码得到z=x+y
