地球椭球
地球椭球体又称地球椭圆体或地球扁球体,代表地球大小和形状的数学曲面,以长半径和扁率表示,因它十分迫近于椭球体,故通常以参考椭球体表示地球椭球体的形状和大小。通常所说地球的形状和大小,实际上就是以参考椭球体的半长径、半短径和扁率来表示。1975年国际大地测量与地球物理联合会推荐的数据为:半长径6378140米,半短径6356755米,扁率1∶298.257。在众多椭球体中,WGS-84椭球体被认为符合上述条件最好的椭球。
基准
所谓基准是指为描述空间位置而定义的点、线和面。而大地测量基准是指用以描述地球形状的地球椭球参数,包含描述地球椭球几何特征的长短半轴和物理特征的有关参数、地球在空间的定位及定向以及描述这些位置所采用的单位长度的定义。不同的坐标系统会使用的基准也不同,根据参考椭球所选原点位置不同,可以分为地心坐标系和参心坐标系。
地心坐标系是以地球的质心为原点,有地心大地坐标系和地心空间直角坐标系两种表述方法。地心空间直角坐标系的定义为:以地球质心为原点,X轴指向格林尼治子午面与地球赤道的交点,Z轴指向北极,Y轴过原点垂直于平面 XOZ,构成右手空间直角坐标系。地心大地坐标系定义为:以地球的质心作为原点,以地球自转轴作为椭球的短轴,大地纬度B是过地面点的椭球法线与椭球赤道面之间的夹角,大地经度L为过地面点的椭球子午面与格林尼治子午面之间的夹角,大地高度H为地面点沿椭球法线到椭球面的最短距离。WGS-84坐标系,CGCS2000坐标系,GLONASS是采用PZ-90坐标,都是属于地心坐标系。
参心坐标系是选取一个参考椭球面作为基本的参考面,选一参考点作为大地测量的起算点,从而确定参考椭球在地球面的位置和方向。这时参考椭球的原点不会和地球质心重合,所以称为参心。北京54坐标系、西安80坐标系和新北京54坐标系,都是参心坐标系。它同样具有参心大地坐标系和参心空间直角坐标系两种表述方法,它们的定义与地心坐标系的定义相似。
我国常用坐标系(基于椭球体分类)
1.1954年北京坐标系
1954年北京坐标系,是采取先将我国一等锁与前苏联远东一等锁相联接,然后以连接处呼玛,吉拉林,东宁基线网扩大边端点的前苏联1942年普尔科沃坐标系的坐标为起算数据,平差我国东北及东部一等锁[10]。椭球参数:长半轴a=6378245m,短半轴b=6356863.0188m,扁率α=1/298.3,第一偏心率平方e2=0.00669342161454287,第二偏心率平方e’2=0.00673852540614652。
2.1980西安大地坐标系
1980国家大地坐标系采用地球椭球基本参数为1975年国际大地测量与地球物理联合会第十六届大会推荐的数据,大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约60公里。椭球参数:长半轴a=6378140±5m,短半轴b=6356755.2882m,扁率α=1/298.257,第一偏心率平方e2 =0.00669438499959,第二偏心率平方e’2=0.00673950181947。
3.WGS-84世界大地坐标系
WGS-84坐标系是一种国际上采用的地心坐标系。坐标原点为地球质心,其地心空间直角坐标系的Z轴指向BIH (国际时间服务机构)1984.0定义的协议地球极(CTP)方向,X轴指向BIH 1984.0的零子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系,称为1984年世界大地坐标系统。椭球参数:长半轴a=6378137,短半轴b=6356752.3142,扁率α=1/298.2572236,第一偏心率平方e2=0.00669437999013 ,第二偏心率平方e’2=0.006739496742227。
4.2000国家大地坐标系
CGCS2000是(中国)2000国家大地坐标系的缩写,该坐标系是通过中国GPS连续运行基准站、空间大地控制网以及天文大地网与空间地网联合平差建立的地心大地坐标系统[11]。Z轴指向BIH1984.0定义的协议极地方向(BIH国际时间局),X轴指向BIH1984.0定义的零子午面与协议赤道的交点,Y轴按右手坐标系确定。椭球参数:长半轴a=6378137,短半轴b=6356752.31414,扁率α=1/298.2572236,第一偏心率平方e2=0.00669437999013 ,第二偏心率平方e’2=0.006739496742227。
测量常用坐标系(基于空间分类)
1.大地坐标系
空间一点的大地坐标用大地经度L、大地纬度B和大地高度H表示,地面上P地点的大地子午面NPS与起始大地子午面所构成的二面角L称P地点的大地经度, P地点对于椭球的法线与赤道面的夹角B称P地点的大地纬度。

2.空间直角坐标系
空间直角坐标系的坐标原点与参考椭球的中心重合,Z轴正向指向参考椭球的北极,X轴正向指向起始子午面与赤道的交点,Y轴按右手系与X轴呈90°夹角且位于赤道面上,某点在空间中的坐标可用该点在此空间坐标系的各个坐标轴上的投影来表示。

3.平面坐标系
平面直角坐标系是利用投影,将空间坐标通过某种数学变换映射到平面上,这种变换称为投影变换[。在我国一般采用的是高斯一克吕格投影,是目前测量上广泛采用的正形投影,特点是没有角度变形,在不同点上的长度比随点位而异,但在同一点上各方向的长度比相同,也称为高斯投影。

4.地方独立坐标系
在我国平面坐标主要采用的是高斯投影,在该投影中,除中央子午线外,其它位置上的任何线段,投影后都会产生一定的长度变形,而且变形随离开中央子午线的距离增加而增加。因此一般采用分带投影的办法,来限制长度变形,我国规定了采用3度带或6度带进行分带投影。在城市、工矿等工程测量中,如果直接在国家分带坐标系中建立控制网,会使地面长度投影的变形较大,当长度变形大于2.5 cm/km时,就难以满足工程上的需要。另一些特殊的测量,比如大桥施工测量,水利水坝测量,滑坡变形监测等,采用国家坐标系精度不能满足工程要求,所以常常会建立适合本地区的地方独立坐标系
坐标转换模型与公式
1.大地坐标系与空间直角坐标系转换模型
将同一坐标系下的大地坐标(B,L,H)转换成空间直角坐标(X,Y,Z)的转换公式为:


式中:a为参考椭球长半轴,e为第一偏心率,N为卯酉圈的半径[12]。
将同一坐标系下的空间直角坐标(X,Y,Z)转换为大地坐标(B,L,H)的公式为:

用公式进行空间直角坐标转换大地坐标时,需要采用迭代计算大地纬度B。具体计算时,可先根据下式求出大地纬度B的初值:

然后利用该初值B代入公式右端tanB中,将等式左边的结果再次代入右端tanB,直到最后两次B值之差小与允许误差为止。当得到大地纬度B后,代入公式即可求出大地高H。
2.高斯正反算转换模型
得到了点的大地坐标(L,B),就可以将其转化为某投影带的高斯平面坐标,我们将椭球参数代入高斯投影正算公式得到更适用于电算的高斯坐标计算的实用公式:

其计算结果的精度可达0. 001m。只要得到了高斯平面坐标(X, Y)后,便可通过高斯反算公式将其转换成大地坐标(B, L),高斯投影反算公式为:

它们的计算精度,即平面坐标可达
3.坐标转换与参数计算转换模型
二维四参数转换模型:

(x1,y1)为某点在A空间直角坐标系中的坐标。(x2,y2)为某点在B空间直角坐标系中的坐标。(🔺x,🔺y)为某点从A空间直角坐标系转换到B空间直角坐标系的两个平移参数。β为从A空间直角坐标系转换到B空间直角坐标系中标系的两个平移参数。β为从A空间直角坐标系转换到B空间直角坐标系中一个旋转参数。m为从A空间直角坐标系转换到B空间直角坐标系中的一个尺度参数。
平面四参数求解步骤如下:
利用公共点计算坐标参数,但至少有两个公共点,当有i个公共点时,可利用最小二乘原理求解参数。
将B直角坐标系中的坐标视为观测值,设A直角坐标系下的坐标视为无误差,列误差方程为:

由于各点的坐标可视为同精度独立观测值,因此P=I。
把各点坐标已知值带入上述误差方程,然后按下列公式求解出四参数:
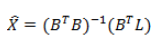
三维七参数转换模型:



七参数求解步骤如下:
利用公共点计算坐标参数,但至少有三个公共点,当有i个公共点时,可利用最小二乘原理求解参数。
将B空间直角坐标系中的坐标视为观测值,设A空间直角坐标系下的坐标视为无误差,列误差方程为:

由于各点的坐标可视为同精度独立观测值,因此P=I。
把各点坐标已知值带入上述误差方程,然后按下列公式求解出七参数:
![]()
实际中完整换算过程
例子:在珠江一个测区,需要完成WGS-84坐标到珠江坐标系(54椭球)的坐标转换,其整个转换过程是:

具体流程是:
a.将WGS84的经纬度转换为WGS84空间直角坐标系下的坐标。
b.用当地三个WGS84和当地坐标(椭球体为BJ54)之间的控制点对,获得七参数。
c.将WGS84的空间直角坐标利用七参数转换到BJ54坐标系下的空间直角坐标。
d.将BJ54的空间直角坐标转换为BJ54的经纬度坐标。
e.对此时BJ54的经纬度坐标进行高斯克吕格投影变为BJ54平面坐标。
f.用当地BJ54下的平面坐标和当地平面坐标之间的两个控制点对得出四参数。
g.将BJ54平面坐标利用四参数转换到当地平面坐标。
