一、获取代码方式
获取代码方式1:
完整代码已上传我的资源:【特征提取】基于matlab基音周期估计【含Matlab源码 551期】
获取代码方式2:
通过订阅紫极神光博客付费专栏,凭支付凭证,私信博主,可获得此代码。
备注:
订阅紫极神光博客付费专栏,可免费获得1份代码(有效期为订阅日起,三天内有效);
二、基音周期估计简介
基音是指发浊音时声带振动所引起的周期性,而基音周期是指声带振动频率的倒数。基音周期是语音信号最重要的参数之一,它描述了语音激励源的一个重要特征。基音周期信息在多个领域有着广泛的应用,如语音识别、说话人识别、语音分析与综合以及低码率语音编码、发音系统疾病诊断、听觉残障者的语言指导等。因为汉语是一种有调语言,基音的变化模式称为声调,它携带非常重要的具有辨意作用的信息。所以,基音的提取和估计对汉语更是一个十分重要的问题。
由于人的声道的易变性及其声道特征的因人而异,而基音周期的范围又很宽,且同一个
人在不同情态下发音的基音周期也不同,加之基音周期还受到单词发音音调的影响,因而基音周期的精确检测实际上是一件比较困难的事情。基音提取的主要困难反映在:①声门激励信号并不是一个完全周期的序列,在语音的头、尾部并不具有声带振动那样的周期性,有些清音和浊音的过渡帧是很难准确地判断是周期性还是非周期性的;②声道共振峰有时会严重影响激励信号的谐波结构,所以,从语音信号中直接取出仅和声带振动有关的激励信号的信息并不容易;③语音信号本身是准周期性的即音调是有变化的),而且其波形的峰值点或过零点受共振峰的结构、噪声等的影响;④基音周期变化范围大,从老年男性的50Hz到儿童和女性的450Hz,接近三个倍頻程,给基音检测带来了一定的困难。由于这些困难,所以迄今为止尚未找到一个完善的方法可以对于各类人群包括男、女、儿童及不同语种)、各类应用领域和各种环境条件情况下都能获得满意的检测结果。
尽管基音检测有许多困难,但因为它的重要性,基音的检测提取一直是一个研究课题。目前的基音检测算法很多, 各有优劣, 如自相关函数ACF) 法、平均幅度差函数A MDF) 法、倒谱法、简化逆滤波法SIFT) 等。
3.1自相关法
语音信号xm)的短时自相关函数R.k)如式5-4)所示,其不为零的范围为k=-N+1)-N-1),且为偶函数。由自相关分析可知,浊音信号的自相关函数在基音周期的整数倍位置上出现峰值;面清音的自相关函数没有明显的峰值出现。因此检测是否有峰值就可判断是清音或浊音,检测峰值的位置就可提取基音周期值。
在利用自相关函数估计基音周期时,有两个需要考虑的问题:窗函数的选取问题和共振
峰的影响问题。窗函数的选取原则如下:
1)无论是利用自相关函数R.k)还是利用平均幅度差函数F,k),语音帧应使用矩形窗。
2)窗长的选择要合适。一般认为窗长至少应大于两个基音周期。而为了改善估计结果,窗长应选的更长一些,使帧信号包含足够多个语音周期。
共振峰的影响问题主要与声道特性相关。有的情况下,即使窗长已选得足够长,第一最大峰值点与基音周期仍不一致,这就是声道的共振峰特性造成的“干扰”。实际上影响从自相关函数中正确提取基音周期的最主要因素是声道响应部分。当基音的周期性和共振峰的周期性混叠在一起时,被检测出来的峰值就会偏离原来峰值的真实位置。另外,某些浊音中,第一共振峰频率可能会等于或低于基音频率。此时,如果其幅度很高,它就可能在自相关函数中产生一个峰值,而该峰值又可以同基音频率的峰值相比拟,从而给基音周期值检测带来误差。为了克服这个困难,可以从两条途径来着手解决:
1)减少共振峰的影响。最简单的方法是用一个带宽为60~900Hz的带通滤波器对语音信号进行滤波,并利用滤波信号的自相关函数来进行基音估计。这个滤波器可以放在对语音信号采样前模拟滤波),也可以放在采样后数字滤波)。将此滤波器的高端截頻置为900Hz,既可以除去大部分共振峰的影响,又可以在基音频率为最高450Hz时仍能保留其一次和二次谐波。低端截频置为60Hz是为了以抑制50Hz的电源干扰。
2)对语音信号进行非线性变换后再求自相关函数。一种有效的非线性变换是“中心削波”,即削去语音信号的低幅度部分。这是因为语音信号的低幅度部分包含大量的共振峰信息,而高幅度部分包含大量的基音信息。
设中心削波器的输人信号为xn),中心削波的输出信号为yn)=C[xn)],则中心削波器如图5-6所示。其中如图5-6a所示的是中心削波函数C[x],一段输入信号xn)及通过中心削波后得到的yn)示例分别如图5-6b和c所示。

图5-6中心削波
a)中心削波函数b)中心前波器的输人e)中心削波器的输出
削波电平C,由语音信号的峰值幅度来确定,它等于语音段最大幅度A…的一个固定百分数。这个门限的选择是重要的,一般在不损失基音信息的情况下应尽可能选得高些,以达到较好的效果。经过中心削波后只保留了超过削波电平的部分,其结果是削去了许多和声道响应有关的波动。中心削波后的语音通过一个自相关器,这样在基音周期位置呈现大而尖的峰值,而其余的次要峰值幅度都很小。计算自相关函数的运算量是很大的,其原因是计算机进行乘法运算非常费时。为此可对中心削波函数进行修正,采用三电平中心削波的方法,如图5-7所示。其输人输出函数为
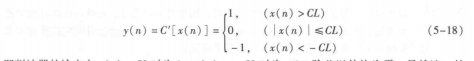
即削波器的输出在xn)>CL时为1,xn)<-CL时为-1,除此以外均为零。虽然这一处理会增加刚刚超过削波电平的峰的重要性,但大多数次要的峰被滤除掉了,而只保留了明显周期性的峰。

图5-8信号波形及其自相关函数举例R,A)均归一化)
a)不波b)中心波c)三电平门波
除了以上的方法外, 还有采用原始语音信号经线性预测LPC) 逆滤波器滤波得到残差
信号后再求残差信号的自相关函数的方法等。近年来,人们还提出了许多基于自相关函数的各种不同的算法, 这些算法或者对自相关函数作适当修改如加权ACF、变长ACF等) , 或者将自相关函数与其他方法相结合如ACF与小波变换相结合、ACF与倒谱相结合等) 。
3.2 平均幅度差函数法
语音信号的短时平均幅度差函数A MDF) F.k) 定义为
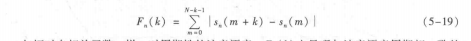
与短时自相关丽数一样,对周期性的浊音语音,F.k)也呈现与浊音语音周期相一致的周期特性,不过不同的是F.k)在周期的各个整数倍点上具有谷值特性面不是峰值特性,因面通过F.k)的计算同样可以来确定基音周期。而对于清音语音信号,F.k)却没有这种周期特性。利用F.k)的这种特性,可以判定一段语音是浊音还是清音,并估计出浊音语音的基音周期。
利用短时平均幅度差函数来估计基音周期, 同样要求窗长取得足够长。可以采取LPC逆滤波和中心削波处理等方法来减少输人语音中声道特性或共振峰的影响,提高基音周期估计效果。近年来许多基于A MDF的不同检测算法被提出。如采用信号经中心削波处理后再计算A MDF函数C-A MDF) 的方法、采用概率近似错误纠正技术的方法、对基本A MDF函数进行线性加权W-A MDF) 的方法、采用变长度A MDF函数LV-A MDF) 的方法、采用原信号经LPC预测分析获得预测残差后再计算残差信号的A MDF函数LP-A MDF)的方法等。
其中W-A MDF定义为

一般的浊音语音的短时A MDF所呈现的周期谷值特性中, 除起始零点F.1) =0) 外,第一周期谷点大多就是全局最低谷点,以全局最低谷点作为基音周期计算点不会发生检测错误。但是, 对于周期性和平稳性都不太好的清音语音段, 基本A MDF的全局最低谷点常常不是第一周期谷点, 多出现在整数倍点的位置处, 如图5-9b所示。这种现象在C-A MDF、W-A MDF、LV-A MDF、LP-A MDF中依然存在, 如图5-9c~f所示。在这种情况下, 若以全局最低谷点作为基音周期计算点就会产生严重的检测错误。解决这一问题的方法之一是采用适当的基音周期计算点的搜索算法, 即在获得A MDF函数的全局最低谷点后进行一定的修正处理,包括:
1)搜索一定取值范围内的局部谷点。
2)比较各候选谷点间的间隔,剔去不满足间隔要求的候选谷点。
3)检查各候选谷点的“清晰度",易去不“清晰”的候选谷点。
4)选定基音周期计算点等。
当然,增加搜索算法后,整个算法的复杂度将增加很多。

由于AMDF的计算无需乘法运算, 因而其算法复杂度较小。另外在基音周期点处AMDF的谷点锐度比ACF的峰点锐度更尖锐, 因此估值精度更高。但是, AMDF对语音信号幅度的快速变化比较敏感,它影响估计的精度。
3.3 倒谱法
倒谱法是传统的基音周期检测算法之一,它利用语音信号的倒频谱特征,检测出表征声
门激励周期的基音信息。
由语音模型可知,语音sn)是由声门脉冲激励en)经声道响应vn)滤波而得,即
sn)=en)*vn)5-22)
设三者的倒谱分别为3n)、en)及n),则有
Sn)=en)+dn)5-23)
可见,包含有基音信息的声脉冲倒谱可与声道响应倒谱分离,因此从倒频谱域分离en)后恢复出en),可从中求出基音周期。然而,反映基音信息的倒谱峰,在过渡音和含噪语音中将会变得不清晰甚至完全消失,其原因主要是因为过渡音中周期激励信号能量降低和类噪激励信号干扰或含噪语音中的噪声干扰所致。对于一帧典型的浊音语音的倒谱,其倒谱域中基音信息与声道信息并不是完全分离的,在周期激励信号能量较低的情况下,声道响应特别是其共振峰)对基音倒谱峰的影响不能忽略。
如果设法除去语音信号中的声道响应信息,对类噪激励和噪声加以适当抑制,倒谱基音检测算法的检测结果将有所改善,特别对过渡语音的检测结果将有明显改善。其中,除去语
音信号中的声道响应信息可采用线性预测方法。在语音信号的线性预测编码LPC) 分析
中,语音信号sn)可以表示为
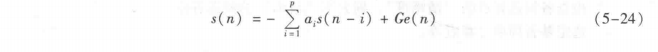
式中,a;为预测系数;p为预测阶数;en)为激励信号;G为幅度因子。如果对输人语音进行LP分析获得预测系数a;,并由此构成逆滤波器Az)
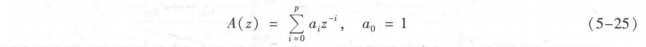
再将原始语音通过逆滤波器Az)进行逆滤波,则可获得预测余量信号:n)理想情况下en)=Gen))。理论上讲,预测余量信号en)中已不包含声道响应信息,但却包含完整的激励信息。对预测余量信号sn)进行倒谱分析,将可获得更为清晰精确的基音信息。在抑制噪声干扰方面,由于语音基音频率一般来说低于500Hz,一个最直观的方法就是对原始语音或预测余量信号进行低通滤波处理。在倒谱分析中,可以直接将傅里叶反变换之前的频域信号的高频分量置零。这样既可实现类似于低通滤波的处理,又可滤去噪声和激励源中的高频分量,减少噪声干扰。
图5-10是一种改进的倒谱基音检测算法。具体步骤包括:1) 对输人语音进行分帧加窗, 然后对分帧语音进行LPC分析,得到预测系数a;并由此构成逆滤波器Az)。

2)将原分帧语音通过逆滤波器滤波,获得预测余量信号en)。
3) 对预测余量信号作傅里叶变换DFT) 、取对数后, 将所得信号的高频分量置零。
4) 将此信号作反傅里叶变换ID FT) , 得到原信号的倒谱。
5)根据所得倒谱中的基音信息检测出基音周期。图5-11是一帧过渡音的倒谱,而
图5-12是在不同信噪比下一帧语音的倒谱。

在由倒谱检测基音周期时,可以直接在倒谱域中根据倒谱的基音峰进行检测;也可以采用倒滤波的方法分离出激励信息,并用逆特征系统将其变换回时域中再进行检测。倒谱域中直接检测的方法算法简单,而逆变换到时域中的方法概念更直观,且在少部分情况下基音峰会变得突出一些。此外,在实际的基音检测算法中,有些情况下需要在检测前作低通滤
波等预处理,并且在基音周期初估以后都要进行基音轨迹平滑的后处理。平滑方法可以
采用中值滤波平滑、“低通”滤波线性平滑等,也可以采用更为有效的诸如动态规划等平滑处理方法。
需要说明的是,倒谱基音检测中,语音加窗的选择是很重要的,窗口函数应选择缓变窗。如果窗函数选择矩形窗,在许多情况下倒谱中的基音峰将变得不清晰甚至消失。一般来

讲,窗函数选择汉明窗较为合理。
3.4 简化逆滤波法
简化的逆滤波跟踪SIFT) 算法是相关处理法进行基音提取的一种现代化的版本。该方法的基本思想是:先对语音信号进行LPC分析和逆滤波, 获得语音信号的预测残差,然后将残差信号通过自相关滤波器滤波,再作峰值检测,进而获得基音周期。语音信号通过线性预测逆滤波器后达到频谱平坦化,因为逆滤波器是一个使频谱平坦化的滤波器,所以它提供了一个简化的频谱平滑器。预测误差是自相关器的输人,通过与门限的比较可以确定浊音。
简化逆滤波器的原理框图如图5-13所示。工作过程为:
- 语音信号经过8kHz取样后, 通过0~900Hz的数字低通滤器, 其目的是滤除声道谱
中声道响应部分的影响,使峰值检测更加容易。 - 然后降低取样率为原来的1/4因为激励序列的宽度小于1kHz, 所以用2kHz取样就足够了)。
- 提取降低取样率后的信号模型参数LPC参数) 。
- 内插提高采样率, 恢复到8kHz。
5)检测出峰值及其位置就得到基音周期值。

在基音提取中,最常采用的是语音波形或误差信号波形的低通滤波,因为这种低通滤波
对提高基音提取精度有良好的效果。低通滤波在除去高阶共振峰影响的同时,还可以弥补自相关函数的时间分辨率的不足。特别是在线性预测误差的自相关函数的基音提取中,误差信号波形的低通滤波处理尤其重要。
3.5 基音检测的后处理
无论采用哪一种基音检测算法都可能产生基音检测错误,使求得的基音周期轨迹中有一个
或几个基音周期估值偏离了正常轨迹通常是偏离到正常值的2倍或1/2),此情况如图5-14
所示。这种偏离点称为基音轨迹的“野点”。

为了去除这些野点,可以采用各种平滑算法,其中最常用的是中值平滑算法和线性平滑
算法。
1 中值平滑处理
中值平滑处理的基本原理是:设xn)为输人信号,yn)为中值滤波器的输出,采用一滑动窗,则n。处的输出值yn,)就是将窗的中心移到n,处时窗内输人样点的中值。即在n。
点的左右各取L个样点。连同被平滑点共同构成一组信号采样值共2L+1)个样值),然后将这2L+1)个样值按大小次序排成一队,取此队列中的中间者作为平滑器的输出。L值一般取为1或2,即中值平滑的“窗口”一般套住3或5个样值,称为3点或5点中值平滑。中值平滑的优点是既可以有效地去除少量的野点,又不会破坏基音周期轨迹中两个平滑段之间的阶跃性变化。
2 线性平滑处理
线性平滑是用滑动窗进行线性滤波处理,即
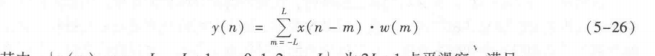
其中,{wm),m=-L,-L+1,…,0,1,2,…,L|为2L+1点平滑窗,满足
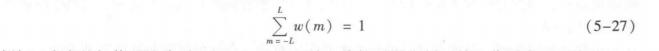
例如三点窗的权值可取为{0.25,0.5,0.25}。线性平滑在纠正输人信号中不平滑处样点
值的同时,也使附近各样点的值做了修改。所以窗的长度加大虽然可以增强平滑的效果,但是也可能导致两个平滑段之间阶跃的模糊程度加重。
3 组合平滑处理
为了改善平滑的效果可以将两个中值平滑串接,图5-15a所示是将一个5点中值平滑和
一个3点中值平滑串接。另一种方法是将中值平滑和线性平滑组合,如图5-15b所示。为
了使平滑的基音轨迹更贴近,还可以采用二次平滑的算法。设所要平滑信号为Tpn),经过
一次组合得到的信号为Tpn)。那么首先应求出两者的差值信号AT,n)=Tpn)-Tpn),
再对AT, n) 进行组合平滑, 得到ATpn) , 令输出等于Tpn) +ATpn) , 就可以得到更好的基音周期估计轨迹。全部算法的框图如图5-15c所示。由于中值平滑和线性平滑都会引人延时,所以在实现上述方案时应考虑到它的影响。图5-15d是一个采用补偿延时的可实现二次平滑方案。其中的延时大小可由中值平滑的点数和线性平滑的点数来决定。例如,一个5点中值平滑将引人2点延时,一个3点平滑将引人1点延时,那么采用此两者完成组合平滑时,补偿延时的点数应等于3。

三、部分源代码
clc; close all; clear all;wlen=640; inc=160; %
T1=0.05; %
p=12; %
[x,fs]=audioread'手放开.wav'); % 读入wav文件
四、运行结果





五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]韩纪庆,张磊,郑铁然.语音信号处理(第3版)[M].清华大学出版社,2019.
[2]柳若边.深度学习:语音识别技术实践[M].清华大学出版社,2019.
