一、指导思想
# 只针对线性回归中的使用
算法的最优模型的功能：预测新的样本对应的值；
什么是最优的模型：能最大程度的拟合住数据集中的样本数据；
怎么才算最大程度的拟合：让数据集中的所有样本点，在特征空间中距离线性模型的距离的和最小；（以线性模型为例说明）
怎么得到最优模型：求出最优模型对应的参数；
怎么求解最优模型的参数：通过数学方法，得到目标函数（此函数计算数据集中的所有样本点，在特征空间中到该线性模型的距离，也就是损失函数），通过批量梯度下降法和随机梯度下降法对目标函数进行优化，得到目标函数最小值时对应的参数；
梯度下降法的目的：求解最优模型对应的参数；（并不是为了求目标函数的最小值，这一点有助于理解随机梯度下降法）
二、批量梯度下降法基础
1）批量梯度下降法的特点
运算量大：批量梯度下降法中的每一项计算：
，要计算所有样本（共 m 个）；
批量梯度下降法的梯度是损失函数减小最快的方向，也就是说，对应相同的 theta 变化量，损失函数在梯度方向上的变化量最大；
2）批量梯度下降法的思路
思路：计算损失函数的梯度，按梯度的方向，逐步减小损失函数的变量 theta，对应的损失函数也不断减小，直到损失函数的的变化量满足精度要求；
梯度计算：变形公式如下
梯度是优化的方向，损失函数的变量 theta 的变化量 = 学习率 X 当前梯度值
三、随机梯度下降法（Batch Gradient Descent）
1）基础理解
思路：随机抽取 n （一般 n = 总样本数 / 3）个样本，在每个样本的梯度方向上逐步优化（每随机抽取一个样本就对 theta 做一次递减优化）变量 theta；
分析：批量梯度下降法的优化，是整体数据集的梯度方向逐步循环递减变量 theta ，随机梯度下降法，是数据集中的一个随机的样本的梯度方向，优化变量 theta；
特点一：直接优化变量 theta，而不需要计算 theta 对应的目标函数值；
特点二：不是按整体数据集的梯度方向优化，而是按随机抽取的某个样本的梯度方向进行优化；
2）优化方向的公式
新的搜索方向计算公式（也即是优化的方向）：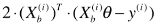
；
此处称为搜索方向，而不是梯度的计算公式，因为此公式已经不是梯度公式，而表示优化损失函数的方向；
随机梯度下降法的搜索路径：
特点：
每一次搜索的方向，不能保证是损失函数减小的方向；
每一次搜索的方向，不能保证是损失函数减小最快的方向；
其优化方向具有不可预知性；
意义：
实验结论表明，即使随机梯度下降法的优化方向具有不可预知性，通过此方法依然可以差不多来到损失函数最小值的附近，虽然不像批量梯度下降法那样，一定可以来到损失函数最小值位置，但是，如果样本数量很大时，有时可以用一定的模型精度，换取优化模型所用的时间；
实现技巧：确定学习率（η：eta）的取值，很重要；
原因：在随机梯度下降法优化损失函数的过程中，如果 η 一直取固定值，可能会出现，已经优化到损失函数最小值位置了，但由于随机的过程不够好，η 又是各固定值，导致优化时慢慢的又跳出最小值位置；
方案：优化过程中让 η 逐渐递减（随着梯度下降法循环次数的增加，η 值越来越小）；
3）η 的确定过程
一：如果 η = 1 / i_iters；（i_iters：当前循环次数）
问题：随着循环次数（i_iters）的增加，η 的变化率差别太大；
二：如果 η = 1 / i_iters + b)；（b：为常量）
解决了 η 的变化率差异过大
再次变形：η = a / i_iters + b)；（a、b：为常量）
分子改为 a ，增加 η 取值的灵活度；
a、b：为随机梯度下降法的超参数；
本次学习不对 a、b 调参，选用经验上比较适合的值：a = 5、b = 50；
学习率的特点
# 学习率随着循环次数的增加，逐渐递减；
# 这种逐渐递减的思想，是模拟在搜索领域的重要思路：模拟退火思想；
# 模拟退火思想：在退火过程中的冷却函数，温度与冷却时间的关系；
一般根据模拟退火思想，学习率还可以表示：η = t0 / i_iters + t1)
4）循环次数的确定
原则
将每个样本都随机抽取到；
将每个样本至少抽取 n 次，也就是总的循环次数一般为：lenX_b) * n；
具体操作
将变形后的数据集 X_b 的 index 做随机乱序处理，得到新的数据集 X_b_new ；
根据乱序后的 index 逐个抽取 X_b_new 中的样本，循环 n 遍；
四、实现随机梯度下降法
优化方向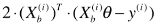：，结果是一个列向量；
# array . dotm) == array . m
eta 取值：η = a / i_iters + b)
优化结束条件
批量梯度下降法：1）达到设定的循环次数；2）找到损失函数的最小值
随机梯度下降法：达到设定的循环次数
随机梯度下降法中不能使用精度来结束优化：因为随机梯度下降法的优化方向，不一定全都是损失函数减小的方向；
1）代码实现随机梯度下降法
模拟数据
import numpy as np import matplotlib.pyplot as plt m = 100000 x = np.random.normalsize=m) X = x.reshape-1, 1) y = 4. * x + 3. + np.random.normal0, 3, size=m)
批量梯度下降法
def Jtheta, X_b, y): try: return np.sumy - X_b.dottheta)) ** 2) / leny) except: return float'inf') def dJtheta, X_b, y): return X_b.T.dotX_b.dottheta) - y) * 2. / leny) def gradient_descentX_b, y, initial_theta, eta, n_iters=10**4, epsilon=10**-8): theta = initial_theta cur_iter = 0 while cur_iter < n_iters: gradient = dJtheta, X_b, y) last_theta = theta theta = theta - eta * gradient if absJtheta, X_b, y) - Jlast_theta, X_b, y)) < epsilon): break cur_iter += 1 return theta
# cur_iter：循环次数
# initial_theta：theta的初始化值
%%time X_b = np.hstack[np.oneslenX), 1)), X]) initial_theta = np.zerosX_b.shape[1]) eta = 0.01 theta = gradient_descentX_b, y, initial_theta, eta) # 输出：Wall time: 898 ms
theta # 输出：array[3.00280663, 3.9936598 ])
随机梯度下降法
1） 通过每一次随机抽取的样本，计算 theta 的优化方向def dJ_sgdtheta, X_b_i, y_i): return X_b_i.T.dotX_b_i.dottheta) - y_i) * 2
# X_b_i：是 X_b 中的一行数据，也就是一个随机样本，不在是全部的数据集
# y_i：对应的随机抽取的样本的真值
2） 随机优化过程 def sgdX_b, y, initial_theta, n_iters): # 计算学习率 eta t0 = 5 t1 = 50 # 定义求解学习率的函数 def learning_ratet): return t0 / t + t1) theta = initial_theta for cur_iter in rangen_iters): rand_i = np.random.randintlenX_b)) gradient = dJ_sgdtheta, X_b[rand_i], y[rand_i]) theta = theta - learning_ratecur_iter) * gradient return theta
# 此处的形参中不需要设置 eta 值了，eta 值随着循环的进行，在函数内部求取
# cur_iter：当前循环次数
# rand_i：从 [0, lenX_b)) 中随机抽取的一个数
# gradient：一次循环中，随机样本的优化方向
# learning_ratecur_iter) * gradient：一次循环的 theta 的变化量
3）给初始化数值，预测数据 %%time X_b = np.hstack[np.oneslenX), 1)), X]) initial_theta = np.zerosX_b.shape[1]) theta = sgdX_b, y, initial_theta, n_iters=lenX_b)//3) # 输出：Wall time: 287 ms
4）查看最终优化结果 theta # 输出：array[2.9648937 , 3.94467405])
2）封装与调用自己的代码
封装：已规范循环次数（代码中的红色字样）
1 def fit_sgdself, X_train, y_train, n_iters=5, t0=5, t1=50): 2 """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型""" 3 assert X_train.shape[0] == y_train.shape[0], 4 "the size of X_train must be equal to the size of y_train" 5 assert n_iters >= 1 6 7 def dJ_sgdtheta, X_b_i, y_i): 8 return X_b_i * X_b_i.dottheta) - y_i) * 2. 9 10 def sgdX_b, y, initial_theta, n_iters, t0=5, t1=50): 11 12 def learning_ratet): 13 return t0 / t + t1) 14 15 theta = initial_theta 16 m = lenX_b) 17 18 for cur_iter in rangen_iters): 19 indexes = np.random.permutationm) 20 X_b_new = X_b[indexes] 21 y_new = y[indexes] 22 for i in rangem): 23 gradient = dJ_sgdtheta, X_b_new[i], y_new[i]) 24 theta = theta - learning_ratecur_iter * m + i) * gradient 25 26 return theta 27 28 X_b = np.hstack[np.oneslenX_train), 1)), X_train]) 29 initial_theta = np.random.randnX_b.shape[1]) 30 self._theta = sgdX_b, y_train, initial_theta, n_iters, t0, t1) 31 32 self.intercept_ = self._theta[0] 33 self.coef_ = self._theta[1:] 34 35 return self
# n_iters：对所有数据集循环的遍数；
调用自己封装的代码
获取原始数据
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets boston = datasets.load_boston) X = boston.data y = boston.target X = X[y < 50.0] y = y[y < 50.0]
数据分割
from ALG.data_split import train_test_split X_train, X_test, y_train, y_test = train_test_splitX, y, seed=666)
数据归一化
from sklearn.preprocessing import StandardScaler standardScaler = StandardScaler) standardScaler.fitX_train) X_train_standard = standardScaler.transformX_train) X_test_standard = standardScaler.transformX_test)
# 数据归一化，主要是将训练数据集（X_train）和测试数据集（X_test）归一化；
使用线性回归算法：LinearRegression
from LR.LinearRegression import LinearRegression lin_reg = LinearRegression) %time lin_reg.fit_sgdX_train_standard, y_train, n_iters=2) lin_reg.scoreX_test_standard, y_test) # 输出：Wall time: 10 ms 0.7865171620468298
# 问题：通过score)函数得到的 R^2 值，也就是准确度过小
# 原因：对所有的 X_train_standard 循环优化的遍数太少：n_iters=2
循环遍数改为 50：n_iters=50
%time lin_reg.fit_sgdX_train_standard, y_train, n_iters=50) lin_reg.scoreX_test_standard, y_test) # 输出：Wall time: 143 ms 0.8085728716573835
循环遍数改为 100：n_iters = 100
%time lin_reg.fit_sgdX_train_standard, y_train, n_iters=100) lin_reg.scoreX_test_standard, y_test) # 输出：Wall time: 502 ms 0.8125954368325295
总结：随着循环遍数的增加，模型的准确度也随着增加；
3）调用 scikit-learn 中的算法模型
SGDRegressor：该算法虽是名为随机梯度下降法的回归器，但其只能解决线性模型，因为，其被封装在了 linear_model 线性回归模块中；
学习scikit-learn中的算法的过程：掉包 – 构建实例对象 – 拟合 – 验证训练模型的效果（查看准确度）
实现过程：前期的数据处理与步骤（2）相同
from sklearn.linear_model import SGDRegressor sgd_reg = SGDRegressor) %time sgd_reg.fitX_train_standard, y_train) sgd_reg.scoreX_test_standard, y_test) # 输出：Wall time: 16 ms 0.8065416815240762
# 准确度为0.8065 左右，此时循环遍数使用默认的 5 遍：max_iter = 5
修改循环遍数：max_iter = 100
sgd_reg = SGDRegressormax_iter=100) %time sgd_reg.fitX_train_standard, y_train) sgd_reg.scoreX_test_standard, y_test) # 输出：Wall time: 8 ms 0.813372455938393
4）总结
与自己写的算法相比，scikit-learn中的算法的实现过程更加复杂，性能更优：
通过计算时间就可以看出：n_iters=100时，自己的算法需要 502ms，scikit-learn中的算法需要 8ms；
自己所学的封装好的算法，只是为了帮助理解算法的原来，而scikit-learn中使用了很多优化的方案