决策树虽然有很多种算法，但是我们基本使用的是CART算法，所以对于决策树，我建议主要深究CART算法就可以 了

一、CART算法介绍

CART（Classification And Regression Tree），看英文名字分类和回归树，就知道该算法既可以用作分类也可以用作回归，我们sklearn中的决策树就是使用CART算法构建的，还有GDBT算法也是。

CART是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART构建决策树用的是二叉树结构，在每个叶节点上预测的是概率分布，也就是在输入给定的条件下输出的条件概率分布。

什么是二叉树，就是每个判断条件只有yes和no这个选择

CART算法由以下两步组成：

（1）决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大；

（2）决策树剪枝：用验证集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

CART决策树的生成就是递归的调用二叉树的过程。对回归树用平方误差最小化准则（mse）或绝对误差最小化准则（mae），对分类树用基尼指数最小化准则，进行特征选择，生成二叉树。

二、回归树生成（均分误差）

输入：训练数据集D

输出：回归树

（1）选择最优切分变量j与切分点s，求解：

                                           

遍历变量j，对固定的切分变量j扫描切分点s，选择使上式达到最小值的对；

CART回归树的度量目标是，对于任意划分特征A，对应的任意划分点s两边划分成的数据集D1和D2，求出使D1和D2各自集合的均方差最小，同时D1和D2的均方差之和最小所对应的特征和特征值划分点，其中，c1为D1数据集的样本输出均值，c2为D2数据集的样本输出均值。

（2）用选定的对（j,s）划分区域并决定相应的输出值：

 其中，由式子可以看出，为节点m中样本的平均值。就是输出值其实就是每个区域的真实值得均值，我们看下面这个例子就很清楚了

 

（3）继续对两个子区域调用步骤（1）,（2），直到满足停止条件；

（4）将输入空间划分为M个区域，生成决策树：
                                         

即，当使用样本进行预测时，样本最终落入的叶节点的均值作为最终的预测值。

三、分类树（基尼系数）

对于离散型数据使用分类树进行预测。分类树基尼指数选择最优的特征，同时决定该特征的最优二值切分点。

基尼系数介绍：

在分类问题中，假设有K个类，样本点属于第k类的概率为，则概率分布的基尼系数定义为：

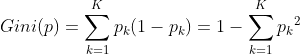
 对于给定样本集合D，其基尼系数为：

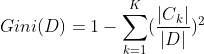
其中，是D中属于第k类的样本子集，K是类别的个数。

如果，样本集合D根据特征A是否取某一可能值a被分割成D1,D2两部分，即：

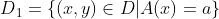
 则在特征A的条件下，集合D的基尼系数为：

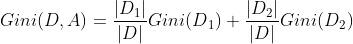
数值越大代表分的越不纯

分类树算法介绍

输入：训练数据集D，停止计算条件；

输出：CART决策树；

根据训练数据集，从根节点开始，递归地对每个节点进行以下操作，构建二叉决策树

（1）计算节点内特征对数据集的基尼系数。此时对每一个特征A，对其可能取的每个值a，根据样本点对A=a的测试为“是”或”否“将D分割成和两个部分，计算A=a时的基尼系数；

（2）在所有可能的特征A以及它们所有可能的切分点a中，选择基尼系数最小的特征及其对应的切分点作为最优特征与最优切分点。依最优特征与最优切分点，从现节点生成两个子节点，将训练数据集依特征分配到两个子节点中去；

（3）对两个子节点递归地调用(1)，(2)，直到满足停止条件（停止计算的条件是节点中的样本个数小于预定阈值，或样本集的基尼系数小于预定阈值，即样本基本属于同一类，或者没有更多特征）；

（4）生成CART决策树。

四、CART树剪枝

由于决策树算法很容易对训练集过拟合，从而导致泛化能力差，为了解决这个问题，我们需要对CART树进行剪枝，即类似于线性回归的正则化，来增加决策树的泛化能力。CART采用的办法是后剪枝法，即先生成决策树，然后产生所有可能的剪枝后的CART树，最后使用交叉验证来检验各种剪枝的效果，选择泛化能力最好的剪枝策略。

也就是说，CART树的剪枝算法可以概括为两步，第一步是从原始决策树生成各种剪枝效果的决策树，第二部是用交叉验证来检验剪枝后的预测能力，选择泛化预测能力最好的剪枝后的树作为最终的CART树。

首先我们看看剪枝的损失函数度量，在剪枝的过程中，对于任意的一刻子树T，其损失函数为：

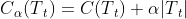
 其中，为正则化参数，这和线性回归的正则化一样。为训练数据的预测误差，分类树是用基尼系数度量，回归树是均方差度量。是子树T的叶子节点的数量。

当时，即没有正则化，原始的生成的CART树即为最优子树。当时，即正则化强度达到最大，此时由原始的生成的CART树的根节点组成的单节点树为最优子树。当然，这是两种极端情况。一般来说，越大，则剪枝剪的越厉害，生成的最优子树相比原生决策树就越偏小。对于固定的，一定存在使损失函数最小的唯一子树。

　　　看过剪枝的损失函数度量后，我们再来看看剪枝的思路，对于位于节点t的任意一颗子树，如果没有剪枝，它的损失是：

         

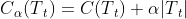
如果将其剪掉，仅仅保留根节点，（也即是1，所以后面的等于a）则损失是：

         

当或者很小时，，当增大到一定的程度时：

                                     

当继续增大时不等式反向，也就是说，如果满足下式：

                                    

和有相同的损失函数，但是节点更少，因此可以对子树进行剪枝，也就是将它的子节点全部剪掉，变为一个叶子节点。

最后我们看看CART树的交叉验证策略。上面我们讲到，可以计算出每个子树是否剪枝的阈值，如果我们把所有的节点是否剪枝的值都计算出来，然后分别针对不同的所对应的剪枝后的最优子树做交叉验证。这样就可以选择一个最好的，有了这个，我们就可以用对应的最优子树作为最终结果。

好了，有了上面的思路，我们现在来看看CART树的剪枝算法。

输入：CART树建立算法得到的原始决策树。

输出：最优决策子树。

算法过程如下：

（1）初始化， 最优子树集合；

（2）从叶子节点开始自下而上计算各内部节点t的训练误差损失函数（回归树为均方差，分类树为基尼系数）, 叶子节点数，以及正则化阈值，更新

（3）得到所有节点的值的集合M。

（4）从M中选择最大的值，自上而下的访问子树t的内部节点，如果时，进行剪枝。并决定叶节点t的值。如果是分类树，则是概率最高的类别，如果是回归树，则是所有样本输出的均值。这样得到对应的最优子树

（5）最优子树集合，；

（6）如果M不为空，则回到步骤4。否则就已经得到了所有的可选最优子树集合；

（7）采用交叉验证在选择最优子树.

求的是a的最小值。

五、决策树算法的优缺点

优点：

（1）决策树很容易理解和解释，而且决策树也容易可视化（在sklearn中可以使用export_graphviz包进行决策树可视化）；

（2）基本不需要预处理，不需要提前归一化，处理缺失值；

（3）决策树在预测时的时间代价是O(logN)，其中N是预测的样本集大小；

（4）能够处理数值型（连续型）和类别型（离散型）的数据。很多其他技术通常在分析数据集的时候只专注于其中一点，即要么是数值型，要么是类别型；

（5）能够处理多维度输出的分类问题，即我们的预测值有多个维度，且多维度是相关的；

（6）决策树使用是作为一个白盒，相较于黑盒的神经网络，决策树在逻辑上可以得到很好的解释；

（7）可以交叉验证的剪枝来选择模型，从而提高泛化能力；

（8）对异常点的容错能力好，健壮性强。

缺点：

（1）决策树容易过拟合，导致模型的泛化能力很差。可以通过剪枝（目前sklearn中的决策树不支持剪枝，所以需要我们自己设置，如叶节点最小值，树的最大深度等），设置每个叶子节点的最小样本数和树的最大深度来避免这个问题；

（2）决策树不稳定，一些很小的变化可能会导致完全不同的决策树生成。这个问题可以通过集成方法来缓解（如：随机森林）；

（3）学习一棵最优化的决策树是NPC问题（就是属于这个的概率p=属于另外类的概率np），因此实际中的决策树学习算法是基于启发式的算法，例如贪心算法在局部做到最优化决策树的每个节点，这样的方法并不能保证能得到一个全局最优的决策树。这个问题可以通过集成的方法来得到改善；

（4）一些复杂的关系决策树很难去学，因为决策树并不能清楚的表达它们，比如，异或问题，多路复用问题等。一般这种关系可以换神经网络分类方法来解决；

（5）如果某些类别的样本比例过大，生成决策树容易偏向于这些类别。因此建议在创建决策树之前要平衡数据集。

六、决策树在sklearn中的一些建议

（1）当数据的特征维度很高而数据量又很少的时候，这样的数据在构建决策树的时候往往会过拟合。所以我们要控制样本数量和特征的之间正确的比率；

（2）在构建决策树之前，可以考虑预先执行降维技术（如PCA，ICA或特征选择），以使我们生成的树更有可能找到具有辨别力的特征；

（3）在训练一棵树的时候，可以先设置max_depth=3来将树可视化出来，以便我们找到树是怎样拟合我们数据的感觉，然后在增加我们树的深度；

（4）树每增加一层，填充所需的样本数量是原来的2倍，比如我们设置了最小叶节点的样本数量，当我们的树层数增加一层的时候，所需的样本数量就会翻倍，所以我们要控制好树的最大深度，防止过拟合；

（5）使用min_samples_split（节点可以切分时拥有的最小样本数） 和 min_samples_leaf（最小叶节点数）来控制叶节点的样本数量。这两个值设置的很小通常意味着我们的树过拟合了，而设置的很大意味着我们树预测的精度又会降低。通常设置min_samples_leaf=5；

（6）当树的类比不平衡的时候，在训练之前一定要先平很数据集，防止一些类别大的类主宰了决策树。可以通过采样的方法将各个类别的样本数量到大致相等，或者最好是将每个类的样本权重之和(sample_weight)规范化为相同的值。另请注意，基于权重的预剪枝标准（如min_weight_fraction_leaf）将比不知道样本权重的标准（如min_samples_leaf）更少偏向主导类别。

（7）如果样本是带权重的，使用基于权重的预剪枝标准将更简单的去优化树结构，如mn_weight_fraction_leaf，这确保了叶节点至少包含了样本权值总体总和的一小部分；

（8）在sklearn中所有决策树使用的数据都是np.float32类型的内部数组。如果训练数据不是这种格式，则将复制数据集，这样会浪费计算机资源。

（9）如果输入矩阵X非常稀疏，建议在调用fit函数和稀疏csr_matrix之前转换为稀疏csc_matrix，然后再调用predict。 当特征在大多数样本中具有零值时，与密集矩阵相比，稀疏矩阵输入的训练时间可以快几个数量级。

文章转载：https://blog.csdn.net/qq_24519677/article/details/82084718?spm=1001.2014.3001.5501